5: Experimental design

Lesinhoud en leerdoelen

Aan het einde van deze les kan je:

• Weten wat data is
• De concepten steekproef en populatie kunnen onderscheiden en eigenschappen benoemen
• Het verschil kennen tussen afhankelijke/onafhankelijke variabele
• Begrijpen wat een controlecondities is
• Weten hoe je een blanco gebruikt tijdens een experiment
• Het verschil kennen tussen technical/biological replicates
• Het verschil kennen tussen gepaarde/ongepaarde groepen

Voorbereiding

Wat is data?

Wat is eigenlijk data, en waarom maken we daar zo’n punt van? Data zijn “units of information”, vaak getallen maar dat hoeft niet, die verzameld zijn en opgeslagen. Dat kan van alles zijn: de staartlengtes van alle katten in Utrecht, welk cijfer (op een schaal van 1-10) alle studenten in je klas de les geven, de gemeten extincties in de laatste vaardighedenles met de spectrofotometer, hoeveel studenten we per leergroep hebben met blond haar, een lijst van alle oscar-nominaties van de afgelopen 5 jaar…

Uit data kun je informatie halen. Vaak wordt dit gezien als het bekijken van patronen in data, of het plaatsen van data in context. Als docent zijn we bijvoorbeeld geinteresseerd in de beoordeling van een les, want uit die data kunnen we informatie halen: vinden studenten de les over het algemeen prettig of niet?

In de loop van je studie ga je een heleboel data verzamelen en bekijken. Maar met data die je niet netjes opslaat of analyseert, kun je later niets mee. De informatie die je er uit had kunnen halen is dan verloren. In deze cursus leer je daarom meer over data en hoe je die kunt bewaren en verwerken met Excel. Ook leer je om die data te visualiseren (bijv. grafiekjes maken), en informatie eruit te halen (beschrijvende statistiek).

Kwalitatieve en kwantitatieve data

Bij data denk je meestal aan getalletjes, en in life sciences zijn dat ook meestal getalletjes die we gemeten hebben. Zoals de concentratie van een stof in een monster. We werken meestal met zulke kwantitatieve data.

Data kun je grofweg verdelen in 2 soorten:

1. kwalitatief: woorden, plaatjes, symbolen etc, deze data kan je alleen tellen, het heeft geen eenheid. Bijvoorbeeld de verschillende haarkleuren van de studenten in VL1224. 2 studenten hebben blond haar en 3 studenten hebben bruin haar.
2. kwantitatief: getallen, deze data kan je meten, het heeft dus ook een eenheid (bijv cm, mL etc). Bijvoorbeeld de inhoud van een waterfles, mijn water fles bevat 500 mL.

Kwalitatieve data

Kwalitatieve data wordt ook wel categorische data genoemd en kunnen we opdelen nominale en ordinale data.

Nominale data

Dit is dat in categorieen, maar de ene categorie is niet hoger of lager dan de andere categorie. Als je bijvoorbeeld vraagt of docenten met de fiets, auto of trein naar de HU komen, dan is hun antwoord (“fiets”, “auto”, “trein”) nominaal. (Let op, als je gaat tellen hoeveel docenten met de auto komen, dan maak je dus discrete kwantitatieve data.)

Ordinale data

Deze data lijkt sterk op nominale data alleen deze keer is er ook nog een rangorde, de ene waarde is groter dan de andere. Bijvoorbeeld als je docenten vraagt of ze er erg lang, lang of kort over doen om op de HU te komen. Lang is meer dan kort, maar hoeveel meer? Geen idee, dat kan je niet opmaken uit dit type data.

Kwantitatieve data

Kwantitatieve data kunnen we onderverdelen in in discrete en continue data.

Discrete data

Dit is data die in hele getallen kunnen worden geteld en geen tussenwaarden hebben. Een voorbeeld hiervan is het aantal huisdieren in je huishouden: bijvoorbeeld 2 of 3. Over het algemeen hebben mensen geen halve cavia’s in huis.

continue data

Dit is gemeten data die elke numerieke waarde kan aannemen. Je kan de waarde in theorie in oneindig kleinere delen opsplitsen. Daarom hebben ze geldige breuk- en decimale waarden. Zoals het gewicht van je kat: bijvoorbeeld 3,2 of 5,328 kilo. Voorbeelden van continue data zijn gewicht, lengte, lengte, tijd en temperatuur.

Naast het onderscheid discreet en continu zijn er nog twee schalen waarin we deze data kunnen uitdrukken. De interval en ratio schaal.

interval schaal

Bij interval data geldt dat niet: een gebouw uit het jaar 2000 is niet 2x zo oud als een gebouw uit het jaar 1000 (de jaartelling is immers een relatieve maat); de hoeveelheid warmte-energie in een voorwerp van 20 graden Celcius is niet twee keer zoveel als in een voorwerp van 10 graden Celcius. Dat komt omdat het nulpunt bij dit soort data niet echt “niks” betekent. Nul uur op de klok is niet “geen tijd”. En in het jaar 0 gebeurde er van alles, er was niet “geen jaar”. De intervallen zijn wel steeds gelijk. Van 15:00h tot 16:00h duurt precies even lang als van 16:00h tot 17:00h.

ratio schaal

Bij ratio data is de verhouding tussen twee uitkomsten een zinvolle grootheid: zo is bv. de lengte van een stuk hout van 2 meter ook 2 keer zo lang als van een stuk hout van 1 meter. 0 meter betekent ook echt nul: niks. Nul gram weegt niets.

Hieronder zie je een diagram die deze opdeling visueel weergeeft.

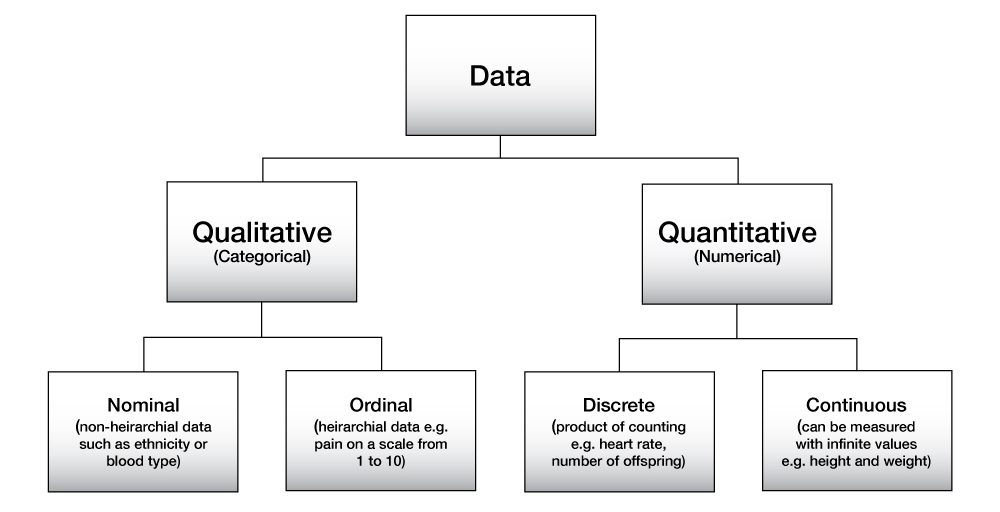
Figure 44: Data opgedeeld in de verschillende soorten.

Bron: Foundations of Biomedical Science: Quantitative Literacy: Theory and Problems Copyright © 2023 by La Trobe University, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Opdracht 5

Welk type data is:

• pH
• goud, zilver en bronzen medailes op de olympische spelen
• bloedgroepen van je leerteam
• aantal van deze vragen dat je fout beantwoordt
• beoordeling van je stoel op een schaal van 1 tot 5 (1 = zit slecht, 5 = zit fantastisch)

Klik hier voor het antwoord

• pH: interval (pH 0 is niet “geen zuurtegraad”, pH 7 is niet 2x zoveel als pH 3.5)
• medailes: ordinaal
• bloedgroepen: nominaal
• aantal vragen fout: ratio (nul fout = niks fout, 4 fout is twee keer zoveel fout als 2 fout.)
• stoelbeoordeling: ordinaal. het zijn wel nummertjes, maar die staan eigenlijk voor kwalitatieve beoordelingen. Ze zijn niet meetbaar. Het interval tussen die nummertjes is niet gelijk: het precieze verschil tussen een score van 2 en een score van 3 is onbekend. 3 is beter dan 2, maar meer kan je niet zeggen. En een stoel met een score van 2 zit niet twee keer zo lekker als een stoel met een score van 1.

Variabelen

In je steekproef zit welke objecten in je populatie je gaat meten (wen je al aan de terminologie?). Maar wat ga je dan meten? Kijk, nu komen we bij de data.

Een variabele is “iets dat kan varieren”, oftewel, het is niet altijd hetzelfde. Als bloedijzerconcentratie altijd bij iedereen exact hetzelfde is, maakt niet uit wat je eet, hoe oud je bent, waar je woont…. dan hoeven we ook geen onderzoek te doen. Welke groepen we ook gaan vergelijken, ze zullen toch niet verschillend zijn.

Voorbeelden van variabelen zijn: lengte, bloeddruk, bloedgroep van proefpersonen, gewicht, IQ, politieke voorkeur, aantal HIV deeltjes in de tijd, uitbraak van influenza virus per regio, grootte van een tumor, hartslag in watervlooien, ijzergehalte in het bloed. Anything!

Variabelen heb je in onderzoek in twee smaken:

De onafhankelijk variabele is wat je weet De onafhankelijk variabele is iets wat je zelf definieert. Een onafhankelijke variabele is bijvoorbeeld de groepsindeling van een experiment (controle vs behandelde groep, man vs vrouw of een tijdsreeks).

De afhankelijke variabele is wat je meet De afhankelijke variabele of “dependent variable” hangt dus af van de onafhankelijke variabele

• populatie: alle objecten (personen, dieren, planten, voorwerpen, cellen, eiwitten enz) waar je vraag over gaat.
• steekproef: (als het goed is random) selectie van n objecten uit een populatie.
• onafhankelijke variabele: wat je weet, iets wat de onderzoeker zelf bepaalt of controleert in het experiment
• afhankelijke variabele: wat je meet, Een meetbaar kenmerk van zo’n object

Opdracht 5

Wat is bij deze onderzoeksvragen de populatie, onafhankelijke en afhankelijke variabele? Wat zou een mogelijke steekproef zijn?

1. onderzoeksvraag: Wat is het effect van verschillende hoeveelheden kunstmest op het bladoppervlak van brandnetels?

Klik voor het antwoord

• populatie: alle brandnetels ter wereld
• onafhankelijke variabele: hoeveelheid kunstmest
• afhankelijke variabele: bladoppervlak
• mogelijke steekproef: stuk of 100 brandnetels (bijvoorbeeld)

2. Onderzoeksvraag: Wat is de gemiddelde staartlengte van de honden in mijn straat?

Klik voor het antwoord

• populatie: alle hondenstaarten in de straat
• onafhankelijke variabele: geen
• afhankelijke variabele: staartlengte
• mogelijke steekproef: misschien is hier een steekproef niet nodig, het lijkt haalbaar om alle hondenstaarten in de straat te meten.

3. Onderzoeksvraag: Zijn mensen in Amersfoort langer dan mensen in Utrecht?

Klik voor het antwoord

• populatie: alle inwoners van Amersfoort en alle inwoners van Utrecht
• onafhankelijke variabele: woonplaats
• afhankelijke variabele: lichaamslengte
• mogelijke steekproef: bijvoorbeeld in beide steden 200 mensen

Gepaarde en ongepaarde data

Gepaarde en ongepaarde data zijn twee belangrijke concepten in statistische analyses, en het is belangrijk om het verschil ertussen te begrijpen.

Gepaarde data: Gepaarde data ontstaan wanneer dezelfde individuen of objecten onder twee verschillende omstandigheden worden gemeten, of wanneer twee nauw verwante metingen worden gedaan. Dit type data wordt vaak gebruikt in “voor en na” studies of in studies waarbij de effecten van twee verschillende behandelingen op dezelfde subjecten worden onderzocht.

Voorbeeld: Stel je een groep van 20 mensen voor die deelnemen aan een dieetprogramma. Hun gewicht wordt gemeten voordat ze met het programma beginnen en opnieuw na drie maanden. Elke persoon heeft dus twee gewichtsmetingen: één vóór en één na het programma. De gewichtsmetingen zijn gepaard, omdat ze voor dezelfde personen gelden en in relatie tot elkaar staan. Hierdoor kunnen we specifieke veranderingen in gewicht per persoon analyseren.

Ongepaarde data: Ongepaarde data worden verzameld wanneer metingen op onafhankelijke groepen of individuen worden gedaan, waarbij er geen directe relatie is tussen de metingen in de verschillende groepen.

Voorbeeld: Stel je een studie voor waarbij het gewicht van 20 mannen en 20 vrouwen wordt gemeten om te bepalen of er een verschil is tussen de gemiddelde gewichten van de twee geslachten. In dit geval zijn de gewichtsmetingen ongepaard, omdat de metingen van de mannen onafhankelijk zijn van die van de vrouwen. Elke groep bestaat uit verschillende individuen, en er is geen onderlinge relatie tussen de individuele metingen van de twee groepen.

In samenvatting worden gepaarde data gebruikt om veranderingen of verschillen binnen dezelfde groep te analyseren, terwijl ongepaarde data worden gebruikt om verschillen tussen onafhankelijke groepen te vergelijken.

Controlecondities en blanco’s

Een controleconditie is een groep in een experiment die dezelfde omstandigheden ervaart als de experimentele groep, behalve de onafhankelijke variabele die wordt getest. Deze groep dient als basislijn om de effecten van de onafhankelijke variabele te meten. Het doel van de controleconditie is om te bepalen of de veranderingen in de afhankelijke variabele daadwerkelijk te wijten zijn aan de onafhankelijke variabele en niet aan andere factoren.

Voorbeeld

In een medicijnstudie krijgt de controleconditie een placebo in plaats van het werkelijke medicijn.

Een blanco, of blanco meting, is een meting die wordt uitgevoerd zonder de aanwezigheid van de variabele of behandeling die wordt getest. Het kan dienen als een nulreferentiepunt. Het doel van een blanco is om achtergrondruis of andere storende factoren te identificeren en te controleren die de resultaten van het experiment kunnen beïnvloeden. Het helpt bij het kalibreren en valideren van de meetinstrumenten.

Voorbeeld

In een chemisch experiment zou een blanco meting een monster bevatten zonder de te meten stof, om te zien hoeveel van de gemeten waarde afkomstig is van andere bronnen dan de stof zelf.

Technische en biologische replicatie

Technische en biologische replicatie zijn beide methoden om variabiliteit in experimenten te controleren, maar ze dienen verschillende doelen en worden op verschillende manieren uitgevoerd.

Technische replicatie betreft het herhalen van dezelfde experimenten onder identieke omstandigheden om variabiliteit te meten die komt uit de experimentele procedure zelf. Dit type replicatie controleert voor fouten en inconsistenties in het proces, zoals pipetteerfouten of machine-afwijkingen. Bijvoorbeeld, meerdere metingen van hetzelfde monster in een experiment zijn technische replicaties. Het doel is om de precisie en betrouwbaarheid van de meetinstrumenten en technieken te beoordelen.

Biologische replicatie daarentegen houdt in dat het experiment wordt uitgevoerd op meerdere, onafhankelijke biologische monsters die representatief zijn voor de populatie of conditie die wordt bestudeerd. Dit kan variabiliteit omvatten die inherent is aan de biologische systemen, zoals genetische verschillen tussen individuele organismen, of omgevingsinvloeden. Bijvoorbeeld, het meten van een bepaalde respons in verschillende muizen zijn biologische replicaties. Het doel hier is om de variabiliteit binnen de biologische systemen te begrijpen en om ervoor te zorgen dat de resultaten generaliseerbaar zijn en niet toevallig of beperkt tot één enkel monster.

Kortom, technische replicatie minimaliseert experimentele ruis, terwijl biologische replicatie de variabiliteit in de biologische systemen onderzoekt, beide cruciaal voor de validiteit en generaliseerbaarheid van wetenschappelijke experimenten.

Onderzoeksvragen aanpakken

We hebben het al eerder gehad over verschillende soorten onderzoeksvragen.

Kwantitatieve onderzoeksvragen (vragen die gaan over iets dat je kunt meten, zie hier) kun je grofweg onderverdelen in drie groepen:

• verschilvragen (bijv: Zijn mannen langer dan vrouwen?)
• verbandvragen (bijv: Wat is het verband tussen hoeveel water per dag gedronken wordt en lichaamslengte bij mannen?)
• beschrijvende vragen (bijv: hoe lang is de gemiddelde Nederlandse man eigenlijk?)

Let op: beschrijvende statistiek over je steekproef doe je daarnaast eigenlijk altijd als je met data werkt. Ook als je een verschilvraag of een verbandvraag hebt. Stel, je vraagt je af of (onderzoeksvraag:) medicijn X het herstel bij griep versnelt ten opzichte van geen medicijnen gebruiken. Dan is het antwoord op je onderzoeksvraag “ja” of “nee”… Maar iedereen wil natuurlijk ook weten hoeveel sneller! Dus vermeld je dan even de gemiddelde ziekteduur in jouw onderzoek met en zonder medicijn X.

• Verschilvragen:
  • is A meer/minder/anders dan B?
  • is A meer/minder/anders dan een verwachte waarde?
  • is A meer/minder/anders dan nul? (is ook een verwachte waarde eigenlijk)
  • etc
• Verbandvragen:
  • als A meer/minder wordt, wordt B dan meer/minder?
  • is er een verband tussen A en B?
  • wat is het effect van A op B?
  • etc
• Beschrijvende vragen:
  • hoeveel is A?
  • hoe zijn A en B verdeeld?
  • etc

Een veelgemaakte fout (op het tentamen en daarbuiten) is een dataset die over een verbandvraag gaat, analyseren alsof het een verschilvraag is (of andersom). Als we ons afvragen wat het verband is tussen waterintake en lichaamslengte bij mannen, willen we geen analyse die gaat kijken of waterintake en lichaamslengte verschillend zijn! Een andere veelgemaakte fout is dan ook: niet heel precies zijn in hoe je zinnen zoals onderzoeksvragen opschrijft. Zoals je ziet maakt het nogal uit. “Wat is het verschil tussen een dood vogeltje?” werkt niet als vraag.

Voorbeeld: De onderzoeksvraag gaat over een verband

Bijvoorbeeld: Is er een verband tussen staartlengte en hoeveelheid blikvoer per dag in Siamezen (katten)?

Variabelen

Heb je een verbandsvraag, dan zijn er dus sowieso 2 variabelen. Die variabelen zijn vaak continue: een continue variabele kan (binnen bepaalde grenzen) iedere waarde aannemen. Lichaamslengte is een voorbeeld van een continue variabele: lichaamslengtes zijn niet beperkt tot hele decimeters (150, 160, 170, 180 cm etc.), je kan 170,2 cm zijn, maar ook 169,89 cm.

Minstens 1 van de twee variabelen meet je. De andere variabele kan je meten of in een experimenteel onderzoek manipuleren. Bij dit katten-voorbeeld kun je kiezen: Je kan van je hele steekproef aan Siamezen achterhalen hoeveel blikvoer ze eten, of je kunt een experiment doen en je steekproef aan Siamezen op een dieet zetten van verschillende hoeveelheden blikvoer.

Grafiek

Data van een verbandsvraag zet je meestal in een scatterplot.

Heb je twee afhankelijke variabelen (dus niks zelf bepaald, alles gemeten), dan maakt het niet uit op welke as welke variabele staat.

Deze kan:

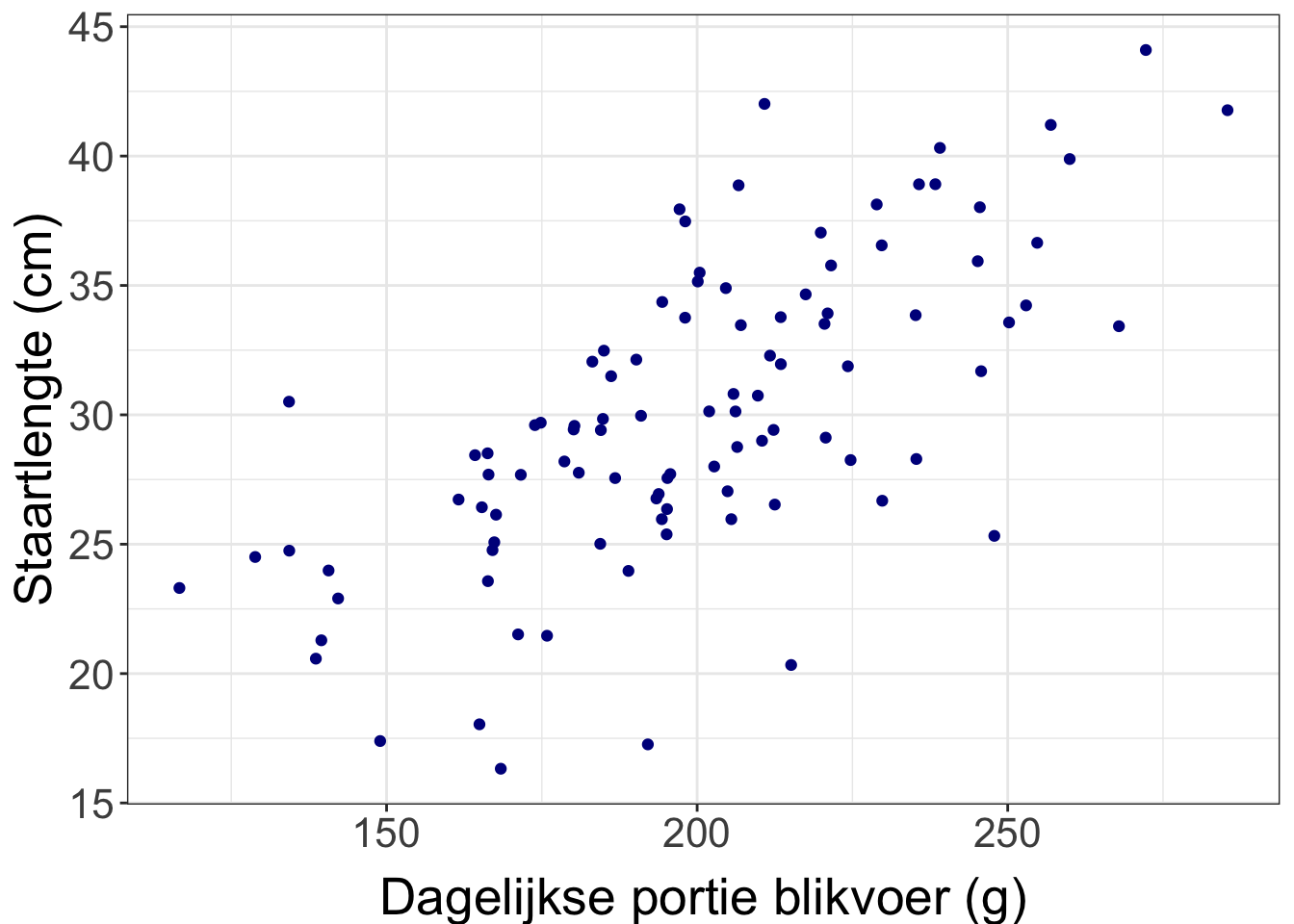
Figure 45: Dagelijkste (niet door ons bepaalde) portie blikvoer en staartlengte van 100 Siamezen.

Maar deze kan ook:

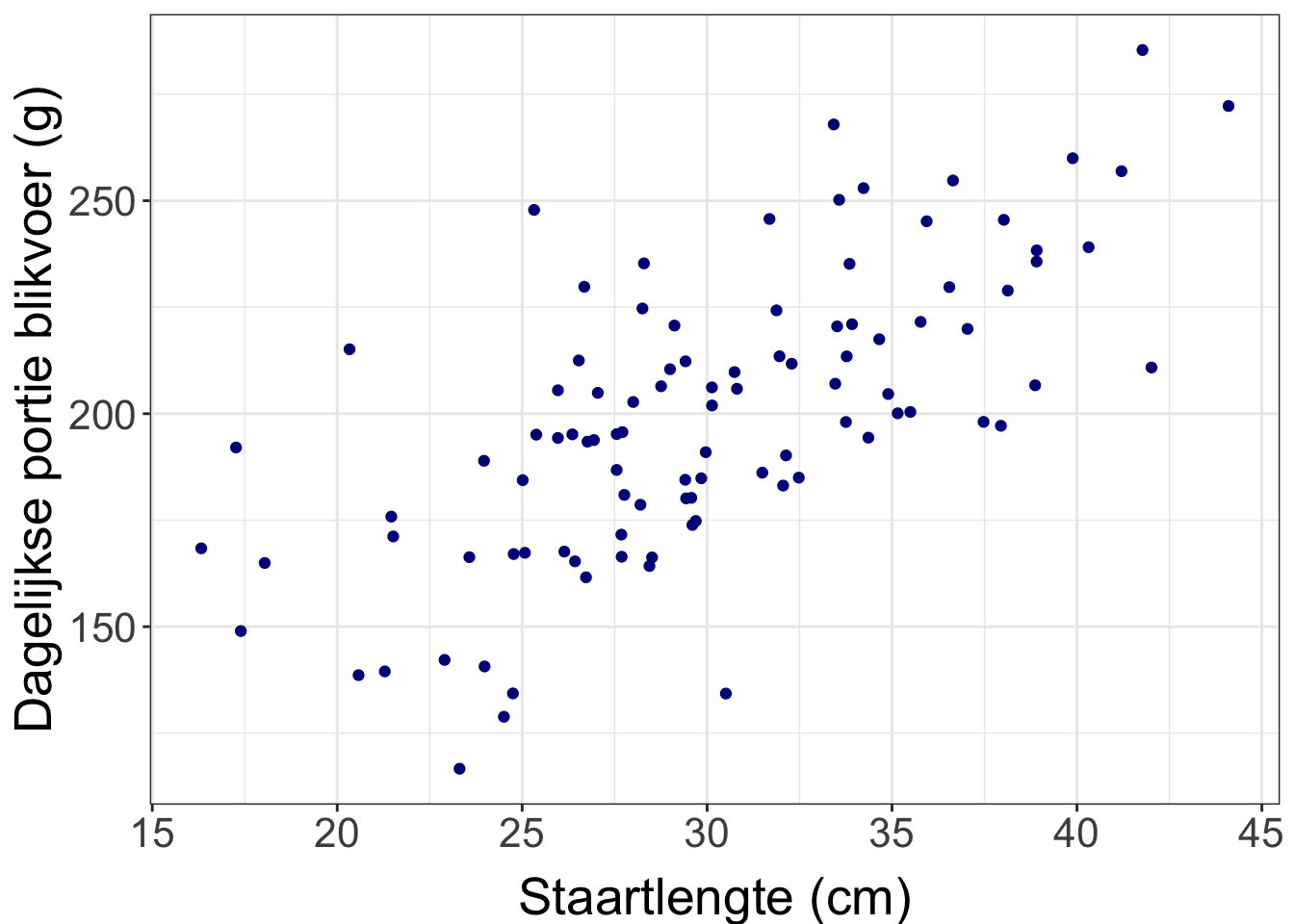
Figure 46: Ook dagelijkste (niet door ons bepaalde) portie blikvoer en staartlengte van 100 Siamezen.

Heb je 1 afhankelijke variabele en 1 onafhankelijke, dan staat de afhankelijke variabele op de Y-as. Zoals bij het voorbeeld van bladgroei tijdens verschillende water conditities. De hoeveelheid millimeter dat een blad gaat groeien hebben wij niet bepaald, het blad groeit uit zichzelf en we meten de groei. Hoeveel het blad zal groeien is afhankelijk van de hoeveelgheid water dat de plant krijgt. Bladgroei is dus de afhankelijke variabele en water consumptie de onafhankelijke. We kiezen zelf hoeveel water een plant krijgt, sommige planten krijgen meer en andere minder, en daarom is deze variabele onafhankelijk.

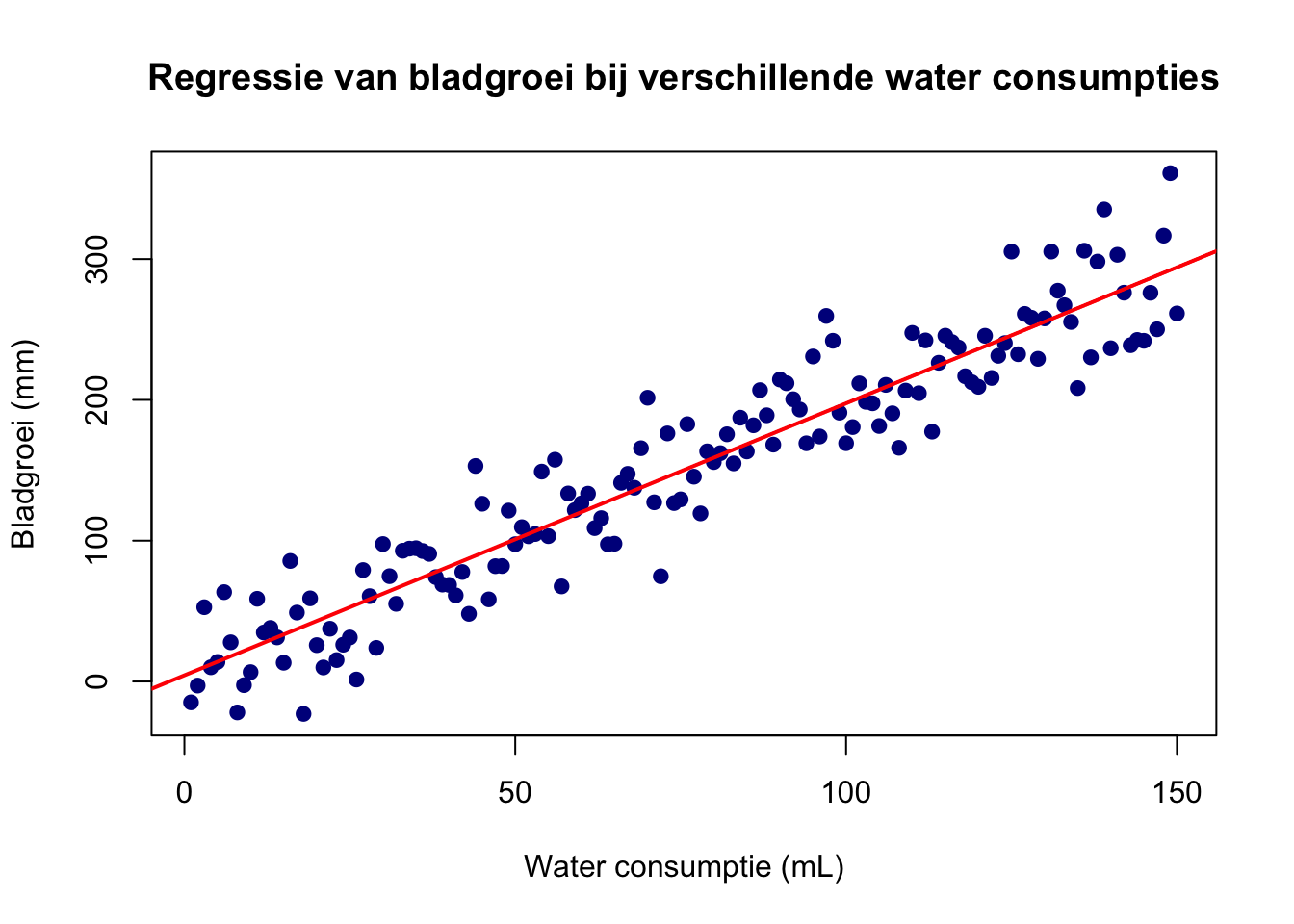
Figure 47: bladgroei bij verschillende waterconsumpties. Elke blauwe stip is de groei van een gemeten blad van 1 plant bij een bepaalde waterconsumptie. De rode lijn is de regressielijn over de totale dataset.

Voorbeeld: De onderzoeksvraag is beschrijvend

Bijvoorbeeld: Hoe lang is de staart van een Siamees?

Je doet 1 steekproef met als afhankelijke variabele “staartlengte”.

Hier kun je alle kanten op, afhankelijk van wat je zou willen laten zien over die staartlengtes. Een mogelijke grafiek voor de beschrijving van kwantitatieve data is een histogram. In een histogram laat je zien hoe vaak bepaalde staartlengtes voorkomen. Op de X-as zie je de staartlengtes, opgedeeld in ranges (15-18 cm, 18-20 cm, 20-22 cm enzovoorts). Op de Y-as zie je hoeveel Siamezen een staartlengte in die range hadden. In totaal zijn 1000 staarten van 1000 Siamezen opgemeten.

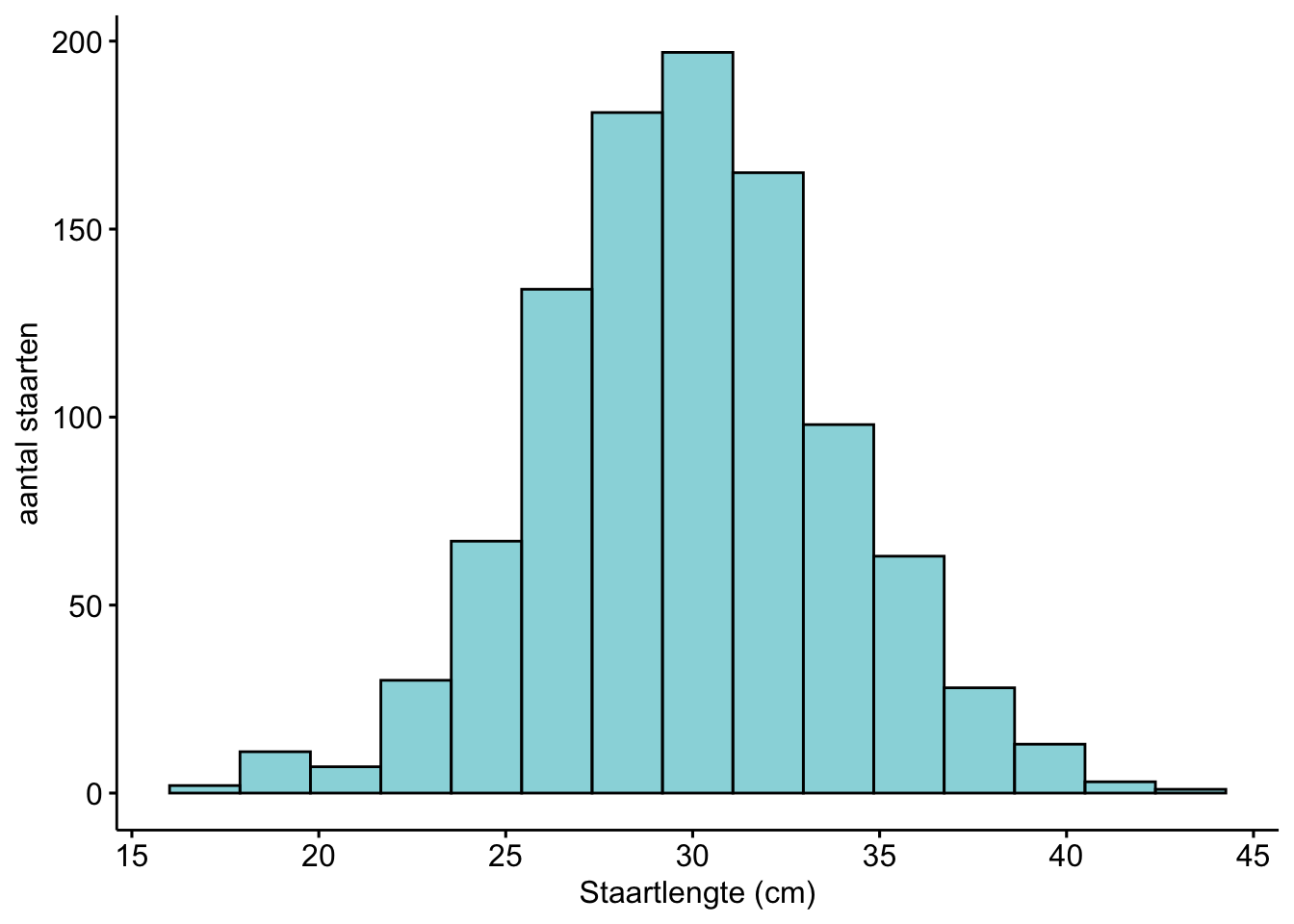
Figure 48: Histogram van 1000 staartlengtes van Siamezen. Te zien is dat de gemiddelde siamezenstaart ongeveer 30 cm is.

Voorbeeld: De onderzoeksvraag gaat over een verschil

Bijvoorbeeld: Hebben Siamezen langere staarten dan Abessijnen (ook katten)?

In het voorbeeld zou je twee steekproeven moeten doen: je moet de staarten van een aantal Siamezen opmeten, en de staarten van een aantal Abessijnen.

Je meet dus 1 afhankelijke variabele: staartlengte. De onanfhankelijke variabele hier is kattenras: Siamees of Abessijn.

(Een verschilvraag kan ook over 1 steekproef gaan. Dan vergelijk je bijvoorbeeld niet Siamezen met Abessijnen, maar Siamezen met de jou bekende gemiddelde staartlengte van Nederlandse katten. Dus in plaats van 2 steekproeven, doe je dan 1 steekproef.)

Bijvoorbeeld een staafdiagram: op de X-as zet je de onafhankelijke variabele (ras). Op de Y-as zet je de afhankelijke variabele (staartlengte in cm). Bij een staafdiagram is de onafhankelijke variabele categorisch. In dit geval nominaal.

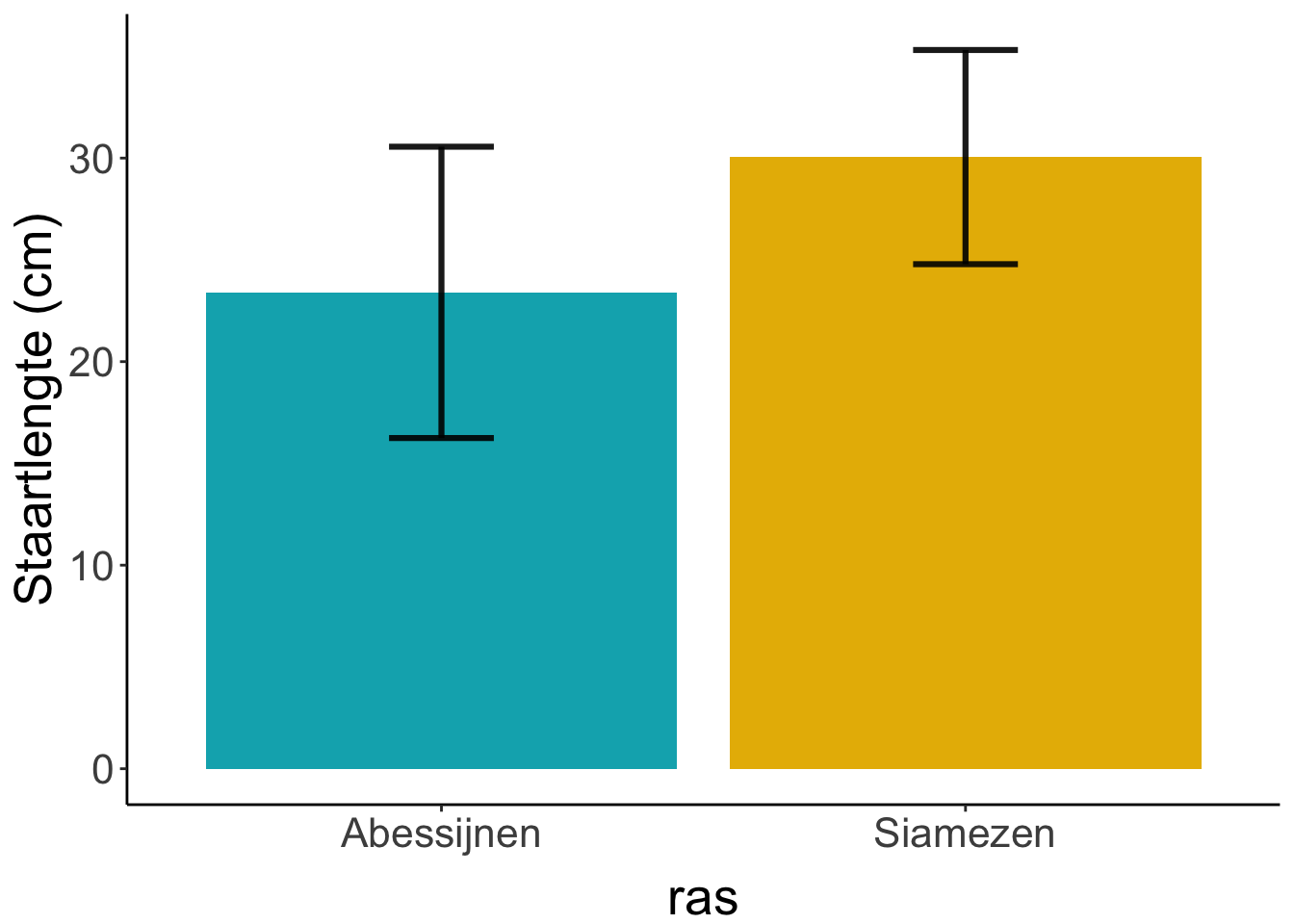
Figure 49: Gemiddelde staartlengte van Abesijnen en Siamezen. In de foutenbalken staat de standaarddeviatie (komt terug in een latere les)

Werkcollege casus experimenteren

Zet een experiment op en gebruik de volgende onderdelen:

Geef aan of je data gepaard is of ongepaard

Geef aan in welke schaal je data is gemeten

Geef aan of je variabelen afhankelijk zijn of onafhankelijk

Bedenk een controle conditie

Geef aan waar je technische en biologische replicatie toepast

Maak hier je eigen dataset voor en visualiseer de resultaten van je experiment