2: Visualisatie

Lesinhoud en leerdoelen

In deze les leren we hoe je data op de juiste manier kunt visualiseren en aan welke regels een goede grafiek moet voldoen. Ook behandelen we hoe je een kalibratielijn kunt opstellen en deze kan gebruiken. En als laatste welke stappen gezet kunnen worden om een uitbijter te testen.

De vaardigheden die je zal verwerven tijdens deze les:

• Weet wat een scatterplot is, hoe je hem maakt en wanneer je deze gebruikt
• Weet wat een lijngrafiek is, hoe je hem maakt en wanneer je deze gebruikt
• Weet wat een histogram is, hoe je hem maakt en wanneer je deze gebruikt
• Kent de algemene regels van grafiek format
• Weet welke grafiekt type hoort bij welke data
• Kan je een kalibratielijn opstellen en deze gebruiken
• Kan je een outlier detecteren en beargumenteren of deze uit de dataset gehaald moet worden

Voorbereiding

Data beschrijven met visualisaties

Het is altijd belangrijk om je data in een grafiek weer te geven. Maar Excel kan een heleboel verschillende grafieken maken. Welke moeten we kiezen? Dat hangt er weer vanaf wat je vraag is. Hieronder een overzicht van een aantal veel gebruikte grafiektypes met argumenten waarom de grafiektypes passen bij de vraag die je stelt.

Scatterplot

Een scatterplot maak je vaak bij een verbandvraag. Bijvoorbeeld: “Is er een verband tussen staartlengte en oorlengte bij de katten in mijn straat?”

Opdracht 2

Open het Excelbestand oorlengtes.xlsx.

en doe mee met de volgende stappen:

• selecteer de kolommen staartlengte en oorlengte.
• kies bovenin de menubalk-tabjes Insert –> charts-blokje –> Selecteer in het submenu Insert - XY scatter een scatter grafiek.

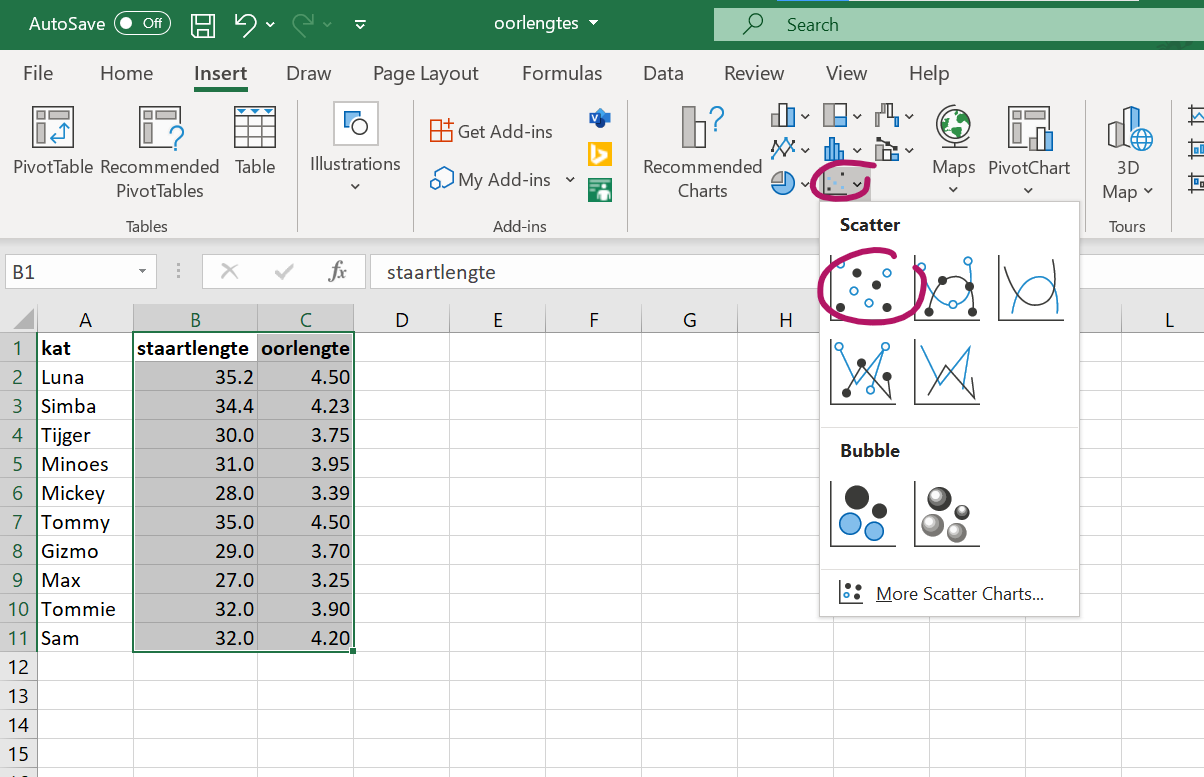
Figure 18: Kies hier echt de met rood aangegeven scatterplots.

• dubbelklik op de grafiektitel en type een betere titel

Figure 19: Grafiektitels moeten goed passen bij wat er in de grafiek staat

• klik nu ergens naast de grafiek in een lege cel, en klik dan in het witte deel van het grafiekje naast de grafiektitel om de hele grafiek te selecteren. Klik daarna links bovenin beeld op Add chart element en voeg asbijschriften toe.

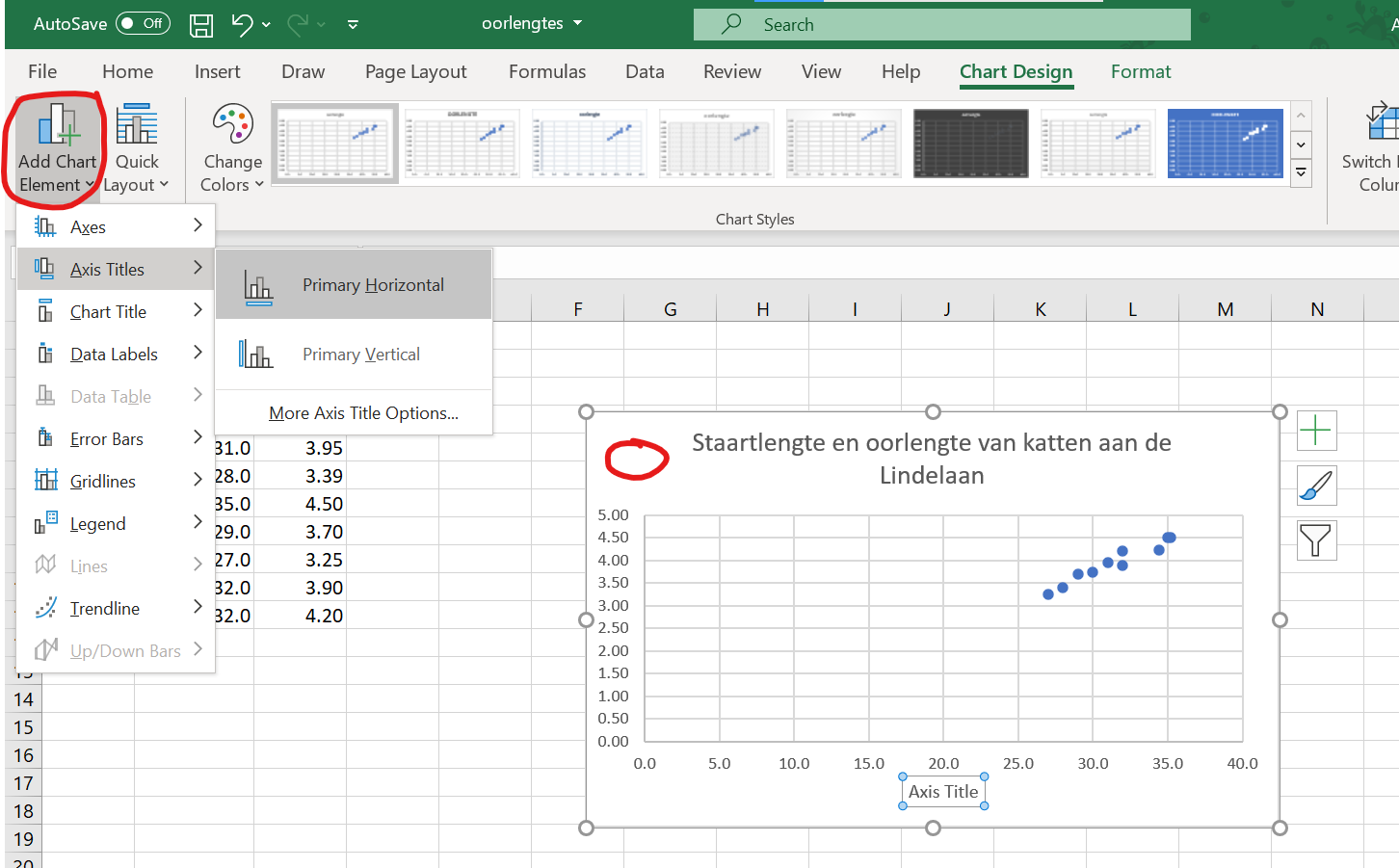
Figure 20: Voeg altijd asbijschriften toe!

• Op de x-as staat staartlengte in centimeters, op de y-as staat oorlengte in centimeters. Grafieken zonder asbijschriften kun je niet aflezen en zullen dus tijdens je hele studie foutgerekend worden!

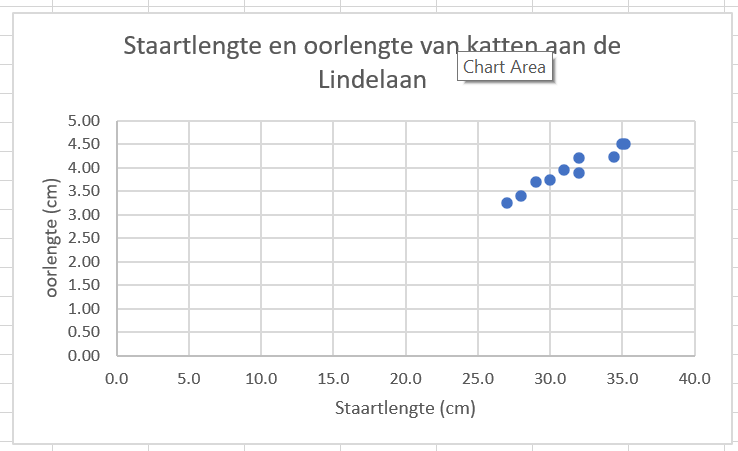
Figure 21: Zo ziet je grafiek er uiteindelijk uit

Staafgrafiek

Voor het beantwoorden van een verschilvraag is een staafdiagram vaak handig en dus ook een veel gemaakte keuze. maar hoe maak je die?

Opdracht 2

Open staartvergelijking.xlsx voor het bestand met kattenstaartlengtes in cm van katten in de Lindelaan en aan de Hoofdweg. Doe de volgende stappen mee:

• Selecteer beide kolommen, klik insert en kies een staafdiagram (zie figuur).

Figure 22: Voorbeeld van hoe een staafdiagram er NIET uit moet zien

Oei. Dat was niet de bedoeling. Elke kat heeft opeens een staaf gekregen. Daar kunnen we niet zoveel mee. We willen graag de gemiddelden kunnen vergelijken.

• Gooi dit grafiekje weer weg!
• De gemiddelde staartlengte voor de katten in de Lindelaan en die voor de Hoofdweg is berekend in cellen A13 en B13. Check met welke formule dit gedaan is.
• Selecteer de twee gemiddelde kattenstaartlengtes en insert een staafdiagram.
• Geef de grafiek astitels en een grafiektitel. Hij ziet er nu zo uit:

Figure 23: Staafgrafek met oninformatieve groepslabels

• Dat ziet er al heel aardig uit, nu moeten die 1 en 2 nog vervangen door de straatnamen. Als je de data waar de grafiek op gebaseerd is wilt aanpassen (in dit geval: labels toevoegen), klik je op chart filters en dan op `select data”

Figure 24: Staafgrafek met oninformatieve groepslabels

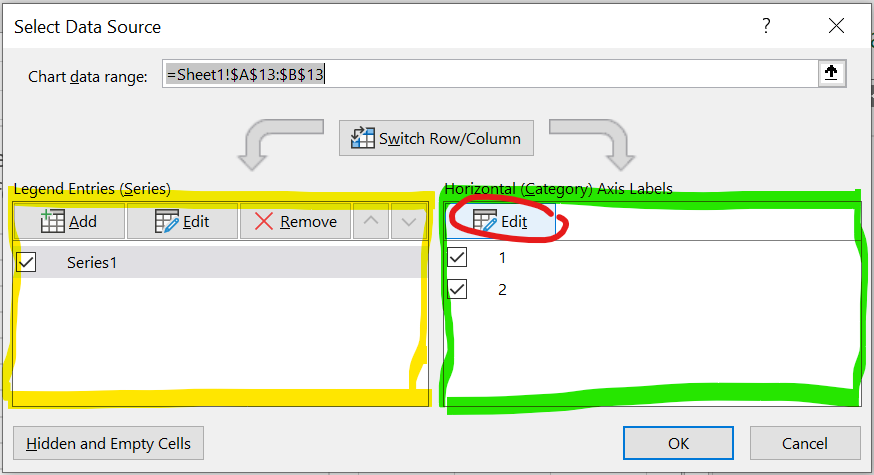
Figure 25: Het Select data source menu.

• in het linker vak zou je de data aan kunnen passen (geel)

• In het rechter vak (groen) kun je de labels aanpassen: klik op edit en selecteer de cellen (beide tegelijk) met de juiste labels, of type : “Lindelaan,Hoofdweg” (als dat niet werkt: “Lindelaan;Hoofdweg”, sommige versies van Excel willen een ; )

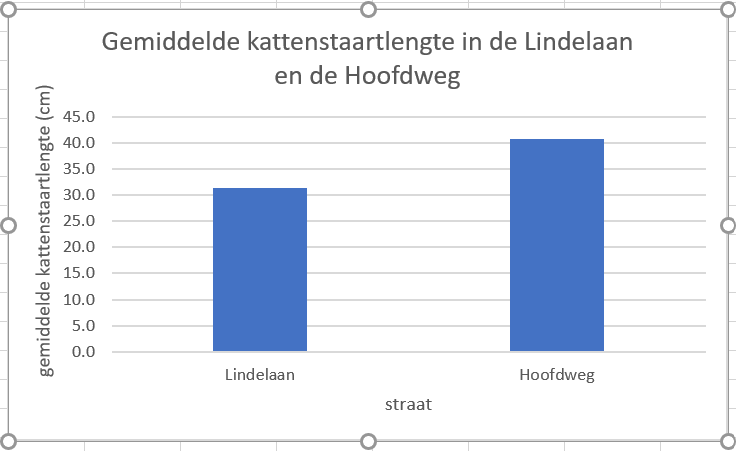
Figure 26: Het staafdiagram aan het eind van deze opdracht.

Hoera, een staafgrafiek!

Sla je Excel-bestand op, we hebben hem komende les nog nodig!

Opdracht 2

Welke katten lijken langere staarten te hebben? Welke informatie kun je in de grafiek niet zien, die je wel nodig hebt om daar echt een inschatting van te kunnen maken?

Klik hier voor het antwoord

Katten aan de Hoofdweg lijken langere staarten te hebben. Maar in de grafiek is niet te zien hoe verschillend kattenstaarten in deze steekproef zijn, er mist een maat voor variatie. Stel je voor dat kattenstaarten kunnen varieren tussen de 10 en 70 cm. De hoeveelheid metingen in deze steekproeven was niet enorm groot. Zou je op basis van 2 maal 10 katten dan al durven inschatten dat katten aan de Hoofdweg langere staarten zouden hebben? Misschien is het verschilletje dat je nu in de grafiek ziet dan wel toeval.. We weten immers al dat als je twee keer een steekproef uit dezelfde populatie zou nemen, je ook niet precies hetzelfde steekproef-gemiddelde zou vinden…

Tja, moeilijk.

In de komende lessen gaan we een maat van spreiding toevoegen aan je grafiek. Dat helpt al.

In jaar 2 gaan we veel verder uitwerken hoe je dit soort vragen kunt beantwoorden, met inductieve statistiek.

Lijngrafiek

Lijngrafieken zijn vooral handig als we veranderingen over veel waarden op de x-as willen laten zien. Dus bijvoorbeeld onze vriend Bas, die kattenstaarten op het Kerkplein al 8 jaar trouw bijhoudt, en elk jaar de gemiddelde kattenstaartlengte berekent:

jaar	gemiddelde staartlengte
2012	25
2013	25.2
2014	26
2015	26.8
2016	32.6
2017	29.5
2018	30.3
2019	31.7
2020	30.9

Een lijngrafiek van deze data doe je door ze naar Excel te kopieren, de kolommen te selecteren, en deze grafiek te kiezen:

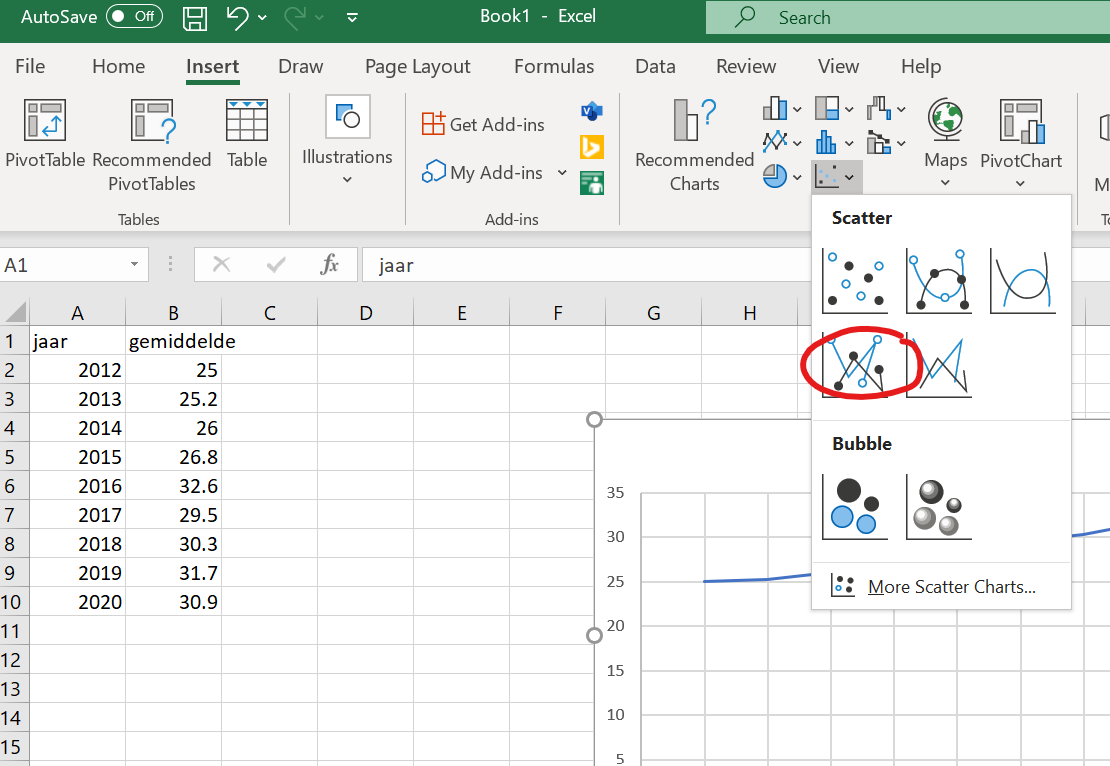
Figure 27: Klik hier voor een lijngrafiek

Probeer de lijn grafiek zelf te maken aan de hand van de stappen hierboven. Denk er aan dat je de grafiek volledig maakt inclusief as-labels, eenheden en zinnige titel.

Algemene regels van grafiek format

Een grafiek bestaat altijd uit een aantal vaste onderdelen, zonder deze onderdelen is de grafiek niet exact af te lezen of te interpreteren. De regels zijn relatief eenvoudig maar alle regels bij elkaar maakt het soms lastig. Onthoud de standaard regels van een grafiek goed ze komen namelijk overal terug in de wetenschappelijke wereld. De onderdelen zijn; as-labels (inclusief eenheid), de titel en legenda.

Op de assen staan de variabelen namen die gebruikt worden in het experiment. In sommige gevallen hebben die variabelen een eenheid zoals temperatuur in graden Celcius. Maar niet altijd, zoals bij het tellen van personen bijvoorbeeld. Je telt gewoon 1 persoon, deze persoon heeft geen eenheid. Zorg er dus voor dat je bij elke as aangeeft over welke variabele het gaat en geef indien mogelijk een eenheid mee.

De titel van een grafiek is een korte volzin die de boodschap van je grafiek overbrengt, probeer hier volledig te zijn. Je rapporteerd naar een ander dus het is belangrijk dat de ander makkelijk begrijpt wat je bedoelt.

Als je meerdere groepen (kleur)codeerd voeg dan een legenda toe zodat het duidelijk is welke kleur voor welke groep staat.

Welke grafiek hoort bij welke data en vraag?

Welke grafiek je gaat maken, hangt voor een groot deel af van wat je je publiek wilt laten zien. Is dat een verschil, of juist heel weinig verschil, of misschien een verband tussen twee dingen? Dat hangt natuurlijk samen met je onderzoeksvraag.

Experimenten doe je niet zomaar uit de losse pols, maar met een gestructureerde planning. Deze structuur: welke variabelen gaan we meten of manipuleren en hoe gaan we die metingen met elkaar vergelijken, vormt de proefopzet. Belangrijk is hierbij dat je met die opzet objectief en zo precies mogelijk een antwoord kunt gaan geven op je onderzoeksvraag.

De proefopzet hangt af van het type onderzoeksvraag. Als je een onderzoek doet, is het belangrijk dat de volgende dingen met elkaar kloppen: je onderzoeksvraag, de variabelen die je meet of manipuleert, en de dingen die je vervolgens met elkaar gaat vergelijken.

Soorten kwantitatieve onderzoeksvragen

Kwantitatieve onderzoeksvragen (vragen die gaan over iets dat je kunt meten, zie hier) kun je grofweg onderverdelen in drie groepen:

• verschilvragen (bijv: Zijn mannen langer dan vrouwen?)
• verbandvragen (bijv: Wat is het verband tussen hoeveel water per dag gedronken wordt en lichaamslengte bij mannen?)
• beschrijvende vragen (bijv: hoe lang is de gemiddelde Nederlandse man eigenlijk?)

Let op: beschrijvende statistiek over je steekproef doe je daarnaast eigenlijk altijd als je met data werkt. Ook als je een verschilvraag of een verbandvraag hebt. Stel, je vraagt je af of (onderzoeksvraag:) medicijn X het herstel bij griep versnelt ten opzichte van geen medicijnen gebruiken. Dan is het antwoord op je onderzoeksvraag “ja” of “nee”… Maar iedereen wil natuurlijk ook weten hoeveel sneller! Dus vermeld je dan even de gemiddelde ziekteduur in jouw onderzoek met en zonder medicijn X.

• Verschilvragen:
  • is A meer/minder/anders dan B?
  • is A meer/minder/anders dan een verwachte waarde?
  • is A meer/minder/anders dan nul? (is ook een verwachte waarde eigenlijk)
  • etc
• Verbandvragen:
  • als A meer/minder wordt, wordt B dan meer/minder?
  • is er een verband tussen A en B?
  • wat is het effect van A op B?
  • etc
• Beschrijvende vragen:
  • hoeveel is A?
  • hoe zijn A en B verdeeld?
  • etc

Een veelgemaakte fout (op het tentamen en daarbuiten) is een dataset die over een verbandvraag gaat, analyseren alsof het een verschilvraag is (of andersom). Als we ons afvragen wat het verband is tussen waterintake en lichaamslengte bij mannen, willen we geen analyse die gaat kijken of waterintake en lichaamslengte verschillend zijn! Een andere veelgemaakte fout is dan ook: niet heel precies zijn in hoe je zinnen zoals onderzoeksvragen opschrijft. Zoals je ziet maakt het nogal uit. “Wat is het verschil tussen een dood vogeltje?” werkt niet als vraag.

Figure 28: Voorbeeld van een dood vogeltje. Rijksmuseum, CC0, via Wikimedia Commons

Opdracht 2

Wat voor soort vraag is dit? Verschil, verband of beschrijvend?

1. Wat is het effect van verschillende hoeveelheden kunstmest op de lengte van brandnetels?

Klik voor het antwoord

verband

2. Zijn brandnetels grotere planten dan dovenetels?

Klik voor het antwoord

verschil

3. Hoeveel groeit mijn muis per dag?

Klik voor het antwoord

beschrijvend

4. Zijn Amsterdammers even zwaar als Utrechters?

Klik voor het antwoord

verschil (“is er geen verschil in gewicht tussen Amsterdammers en Utrechters?”)

5. Zijn mensen in Zwolle gemiddeld 1,75 meter lang?

Klik voor het antwoord

verschil

(“Is er een verschil tussen de lengte van mensen in Zwolle en 1,75?” Oftewel: je hebt een verwachte waarde, en je vraagt je af of de populatie anders is (verschilt) dan die verwachte waarde of niet.)

6. Hoe lang zijn mensen in Amersfoort?

Klik voor het antwoord

beschrijvend

(Hier verwacht je verder niets, geen specifieke verschil- of verband-vraag, je wilt alleen beschrijven)

Voorbeeld: De onderzoeksvraag gaat over een verband

Bijvoorbeeld: Is er een verband tussen staartlengte en hoeveelheid blikvoer per dag in Siamezen (katten)?

Data van een verbandsvraag zet je meestal in een scatterplot. We gaan verderop in de les kijken hoe je die maakt in Excel. Heb je een van beide variabelen gemanipuleerd in een experiment in plaats van gemeten, dan staat die variabele altijd op de X-as. Wat je meet, zet je op de Y-as. Heb je niks bepaald en alleen maar gemeten, dan maakt het dus niet uit welke je op de X- en Y-as zet.

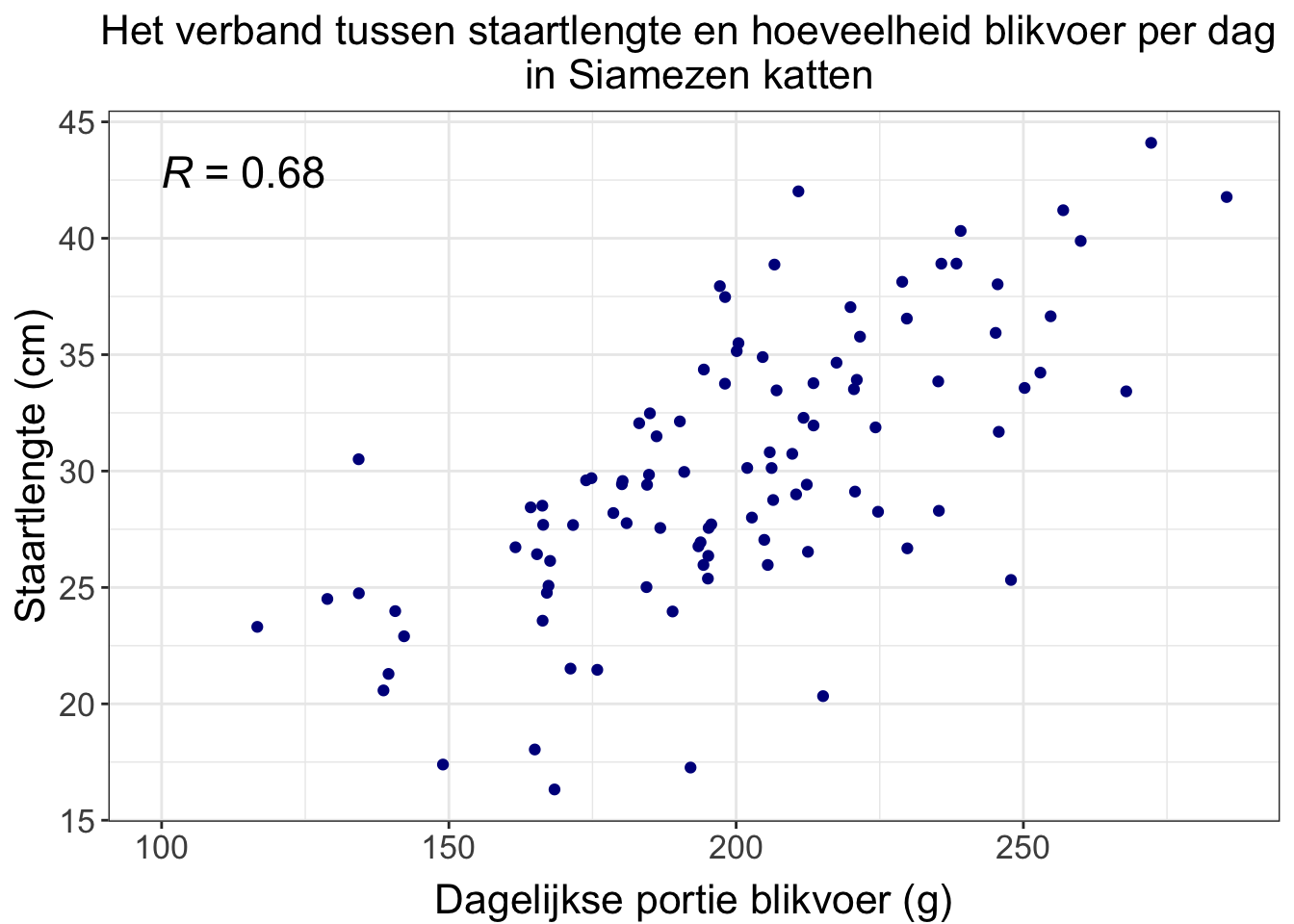
Figure 29: Dagelijkste portie blikvoer en staartlengte van 100 Siamezen. Elk stipje is een Siamees. Te zien is dat Siamezen die meer blikvoer eten, langere staarten lijken te hebben. Die R links in beeld zegt iets over de sterkte van die verband, dit behandelen we in een volgende les. (Dit is verzonnen voor het voorbeeld, ik verwacht niet een dergelijk sterk verband tussen hoeveelheid blikvoer en staartlengte in real live.)

Voorbeeld: De onderzoeksvraag is beschrijvend

Bijvoorbeeld: Hoe lang is de staart van een Siamees?

Hier kun je alle kanten op, afhankelijk van wat je zou willen laten zien over die staartlengtes. Een mogelijke grafiek voor de beschrijving van kwantitatieve data is een histogram. In een histogram laat je zien hoe vaak bepaalde staartlengtes voorkomen. Op de X-as zie je de staartlengtes, opgedeeld in ranges (15-18 cm, 18-20 cm, 20-22 cm enzovoorts). Op de Y-as zie je hoeveel Siamezen een staartlengte in die range hadden. In totaal zijn 1000 staarten van 1000 Siamezen opgemeten.

Figure 30: Histogram van 1000 staartlengtes van Siamezen. Te zien is dat de gemiddelde siamezenstaart ongeveer 30 cm is.

Zorg dat je het histogram hierboven begrijpt. Het is een heel veel gebruikte vorm van visualiseren.

Bij beschrijvende vragen in andere situaties kun je ook hele andere grafieken tegenkomen, zoals lijngrafieken, boxplots, of zelfs taartdiagrammen (al zouden we die meestal niet aanraden, zie ook hier).

Voorbeeld: De onderzoeksvraag gaat over een verschil

Bijvoorbeeld: Hebben Siamezen langere staarten dan Abessijnen (ook katten)?

Je zou best 2 van die histogrammen in hetzelfde grafiekje kunnen maken: 1 histogram voor de siamezen en 1 histogram voor de abessijnen.

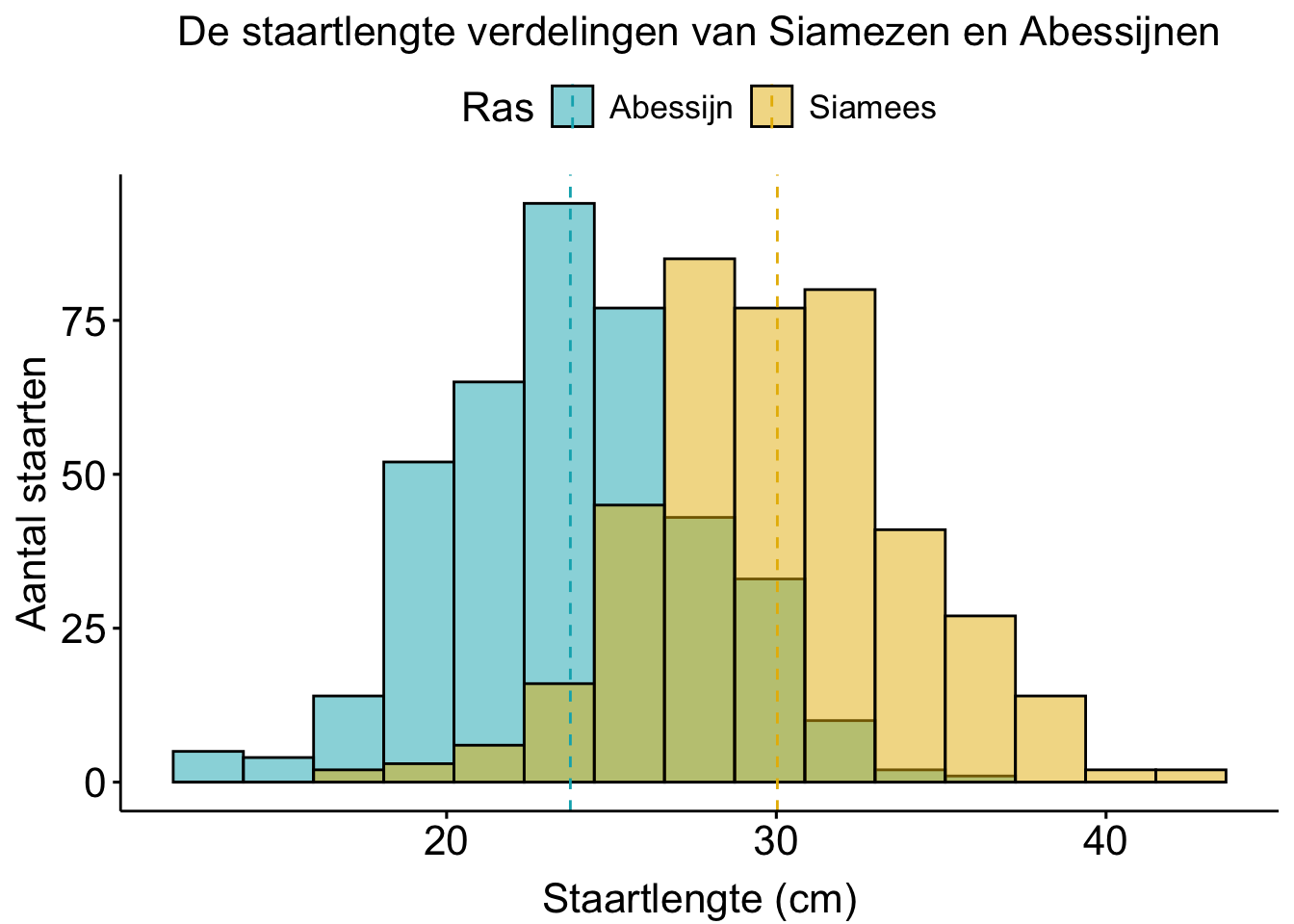
Figure 31: Histogram van de staartlengtes van Siamezen. Te zien is dat de gemiddelde siamezenstaart ongeveer 30 cm is.

Maar gebruikelijker is om een staafdiagram te maken. In een staafdiagram geef je dan het gemiddelde staartlengte per ras weer (de gestippelde lijn in het histogram hierboven, in het staafdiagram hieronder is dat de hoogte van de staaf) en een indicatie van hoe breed die histogrammen dan zijn (dat streepje met twee dwarsbalkjes bovenop de staaf). Dat zegt dus iets over hoe verschillend de staartlengtes bij dat ras zijn: de spreiding. We gaan in volgende lessen bespreken op welke manier je spreiding kunt uitdrukken en hoe je dat in een grafiekje zet.

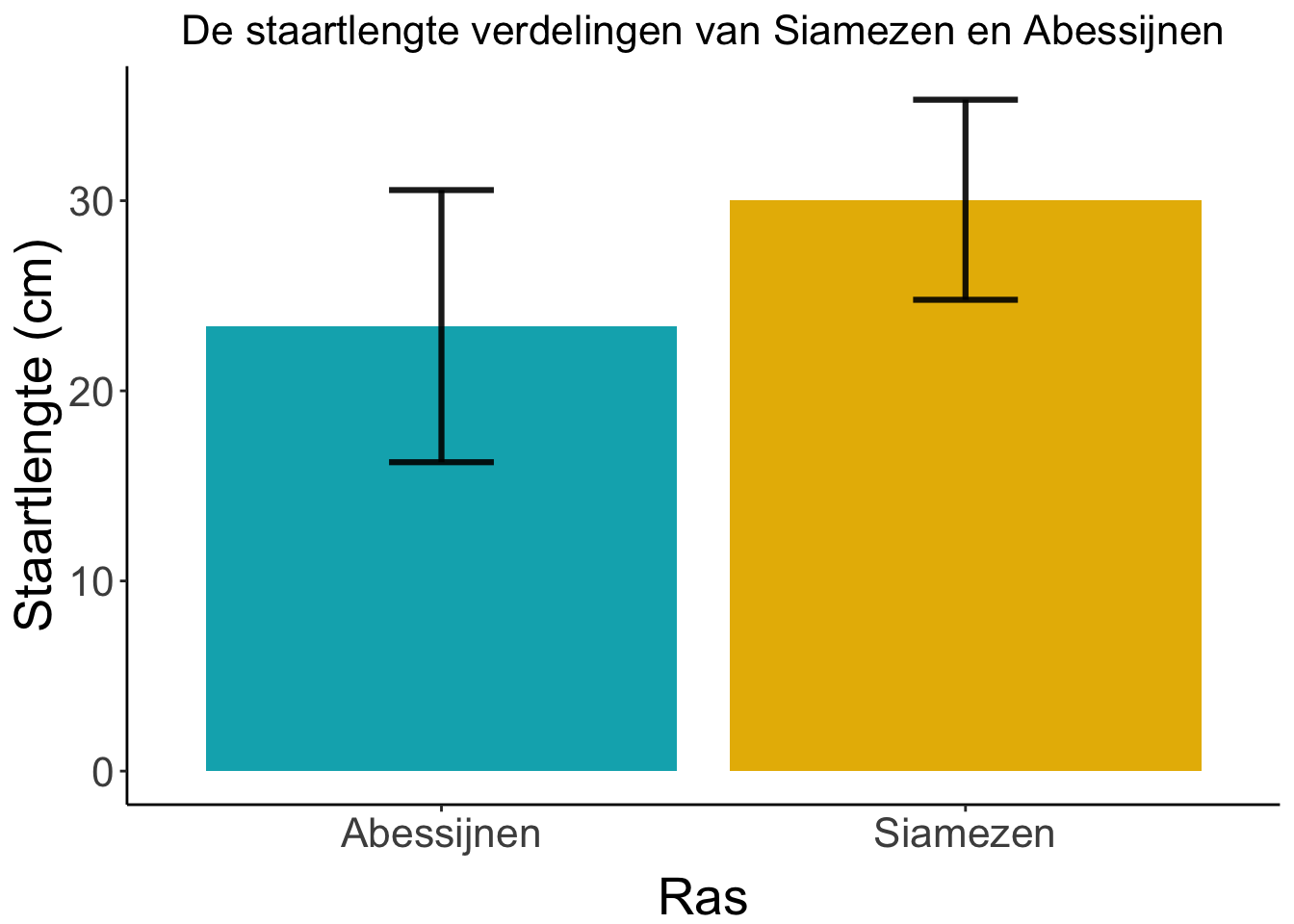
Figure 32: Gemiddelde staartlengte van Abesijnen en Siamezen. In de foutenbalken staat de standaarddeviatie (komt terug in een latere les)

Kalibratielijn opstellen en gebruiken

Een veel voorkomend voorbeeld van een verbandvraag is wat je doet als je een kalibratielijn maakt bij fotospectrometrie:

Voor het bepalen van de hoeveelheid glucose in een bloedmonster maak je gebruik van een chemische reactie waarbij het reactiemengsel een rode kleur krijgt in aanwezigheid van glucose. De hoeveelheid rode kleur die ontstaat kun je meten met een spectrofotometer. Om aan de hand de absorptie vervolgens de concentratie glucose te kunnen bepalen, zul je eerst aan de hand van oplossingen met bekende glucose concentraties moeten vaststellen wat het verband is tussen de concentratie glucose en de extinctie. Met andere woorden, je zult een kalibratielijn moeten opstellen. De kalibratielijn wordt in een volgende les uitgebreid behandeld, maar omdat jullie hem al snel in het lab gaan tegenkomen maken we er nu alvast een.

De data

In het kort, van een bekende concentratie glucose worden verdunningen gemaakt en van deze verdunningen worden na een chemische reactie de extincties gemeten m.b.v een spectrofotometer. De gemeten extincties worden uitgezet tegen de bekende concentraties glucose in de verdunde oplossingen (Rode stippen). Vervolgens laat je het bloedmonster met de onbekende concentratie glucose dezelfde reactie ondergaan en je meet de extinctie (Paarse stip).

Figure 33: Zo ziet je grafiek er uiteindelijk uit

Opdracht 2

In deze eerste opdracht ga je zelf een kalibratielijn opstellen en de concentratie van glucose in een onbekende oplossing bepalen.

We beginnen met de kalibratielijn. Hiervoor werd van vier bekende concentraties glucose de extinctie drie keer gemeten (in triplo dus).

Open het bestand eerste_calibratielijn.xlsx

Bereken de gemiddelde extincties per concentratie in kolom F (oranje vakjes)

Tip: je kunt de formule typen in de bovenste oranje cel (F3) en dan kopieren naar de cellen er onder door op de rechtsonderhoek op het zwarte blokje te klikken (je muiswijzer wordt een zwart kruisje) en naar beneden te slepen.

Figure 34: klik hier en sleep om een formule te kopieren naar de cellen er onder. Je kunt ook dubbelklikken op het zwarte blokje, dan vult Excel de tabel vanzelf aan.

Maak nu een scatterplot met concentratie op de x-as en gemiddelde extinctie op de y-as. Vergeet de titel en asbijschriften niet. Een geschikte titel is hier bijvoorbeeld “kalibratielijn glucose”.

Je kunt twee kolommen data selecteren door CTRL te gebruiken:

• selecteer cel B3 tot en met B6
• druk CTRL en houd ingedrukt
• selecteer F3 tot en met F6
• kies insert en voeg een scatterplot toe

Nu hebben we een scatterplot, maar we kunnen de blauwe vakjes nog niet invullen! Daarvoor moeten we kunnen omrekenen van extinctie naar concentratie glucose. Oftewel, we hebben een formule nodig. Excel kan voor je berekenen wat de meest waarschijnlijke formule is. We gaan in een van de komende lessen zien hoe Excel dat aanpakt.

Opdracht 2

• Windows: klik op je grafiek om hem te selecteren en klik dan op het kruisje rechtsbovenin. Kies trendline en klik op het pijltje naar rechts en dan op “more options”
• Mac: (niet op plaatje) klik op een van de punten in je grafiek. ctrl-click (rechter muisklik) en kies add trendline.

Figure 35: klik hier om de kalibratielijn toe te voegen

• Windows: klik dan op trendline options, scroll omlaag en vink Display equation on chart en Display R-squared value on chart. Dat eerste is de formule, dat tweede is een maat voor hoe goed je kalibratielijn is. 1 is uitstekend.

• Mac: Vink in het menu rechts aan: Display equation on chart en Display R-squared value on chart. Dat eerste is de formule, dat tweede is een maat voor hoe goed je kalibratielijn is. 1 is uitstekend.

Als het goed is, dan heb je de volgende relatie tussen de concentratie en extinctie gevonden:

y=0.0246x + 0,0041.

Y is de extinctie (die staat op de y-as in je grafiek) en x is de concentratie (die staat op de x-as in de grafiek).

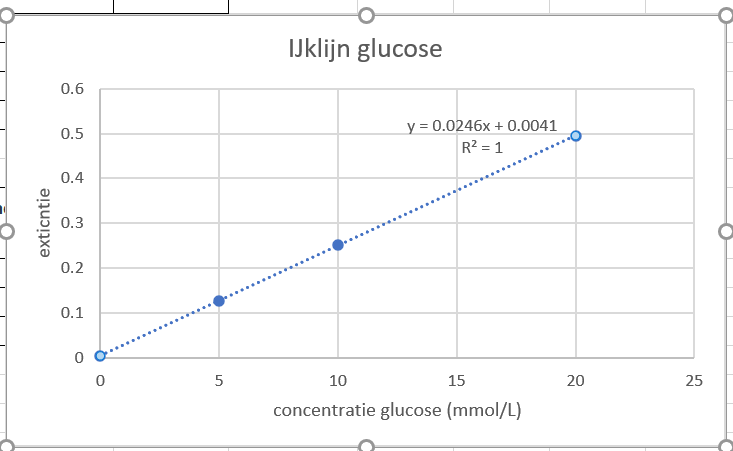
Figure 36: Als het goed is ziet je grafiek er nu zo uit

Van de monsters van de proefpersonen is y (extincties) bekend. Met de gevonden formule kun je de x, de concentraties, berekenen. We moeten hem alleen even omdraaien.

Opdracht 2

Hoe kun je de formule van de kalibratielijn y=0.0246x + 0.0041 omschrijven zodat je de concentratie x kunt uitrekenen wanneer y bekend is?

\[0.0246x = y+0.0041\]

of

\[ x = \frac{y}{0.0246} - 0.0041 \]

of

\[ x = \frac{y - 0.0041}{0.0246} \]

Klik voor het antwoord

\[ x = \frac{y - 0.0041}{0.0246} \]

Opdracht 2

Bereken de gemiddelde extincties van de proefpersonen (groene cellen).

Gebruik de formule uit de vorige vraag om die gemiddelde extincties om te rekenen naar concentraties (blauwe cellen). Rond de waardes af op net zoveel significante cijfers als de extinctiemetingen.

Als je ze in Excel met het goede aantal significante cijfers weergegeven wilt hebben (Excel onthoudt stiekem gewoon alle cijfers), gebruik dan deze knoppen:

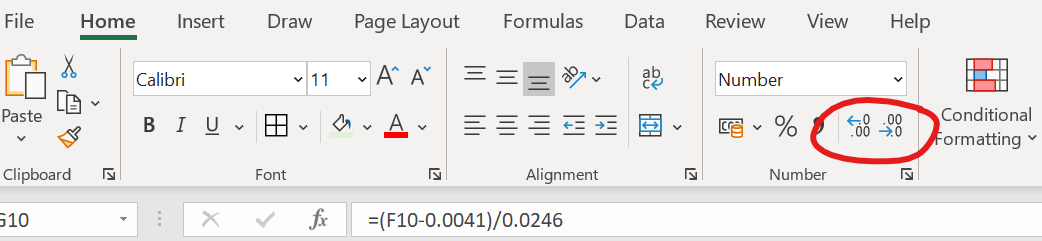
Figure 37: Knoppen om meer of minder decimalen TE LATEN ZIEN in Excel

Klik voor het antwoord

De formule was \[ x = \frac{y - 0.0041}{0.0246} \]

• Selecteer de cel rechts van de gemiddelde extinctie van proefpersoon Jeroen. In ons voorbeeld is dit cel G10.
• Voer het volgende in: =(F10-0.0041)/0.0246
• Selecteer opnieuw cel G13 en beweeg met je muis naar de rechteronderhoek van de cel totdat een zwart kruisje verschijnt. Druk op de linker muisknop en sleep de muis naar beneden zodat de glucose concentratie ook voor de andere proefpersonen berekend wordt.

De concentraties zijn 14.9 , 4.71, 32.4 en 2.11 mmol/L (vergeet de eenheid niet).

Opdracht 2

EXTRA oefenopdracht

In een experiment wordt de hoeveelheid cholesterol in triplo gemeten in patiëntenmonsters. De gemeten extincties zijn als volgt:

Patient	Extinctie 1	Extinctie 2	Extinctie 3
Ronald	0.338	0.315	0.271
Ivo	0.103	0.092	0.125
Erica	0.210	0.198	0.242
Ans	0.268	0.285	0.258

Om de cholesterol concentraties te kunnen berekenen, dien je eerst een kalibratielijn op te stellen.

Stel de kalibratielijn op aan de hand van de volgende meetwaarden en vergeet niet om de kalibratielijn formule weer te geven in je grafiek

Concentratie cholesterol (mmol/L)	Extinctie 1	Extinctie 2	Extinctie 3
0	0.002	0.003	0.006
2.5	0.135	0.145	0.138
5	0.278	0.286	0.281
10	0.521	0.578	0.533

Bereken de concentraties cholesterol in de verschillende patientenmonsters en rond deze af op 3 decimalen

Klik voor het antwoord

Patient	concentratie
Ronald	5.591 mmol/L
Ivo	1.870 mmol/L
Erica	3.903 mmol/L
Ans	4.895 mmol/L

Uitbijters bij herhaalde metingen

Soms is een waarde zo afwijkend dat het de vraag is of je die wel mee moet nemen in je verdere analyse. De vraag is dan dus hoe (on)waarschijnlijk die meting is.

Stel, je bepaalt de concentratie van een stof in een bloedmonster afkomstig van een proefdier in vijfvoud; je vindt de waarden 4,4; 5,3; 4,4;4,6 en 4,6. (Vaak meet je een grootheid een aantal malen om nauwkeurige(r) uitspraken te kunnen doen over de gemiddelde waarde.)

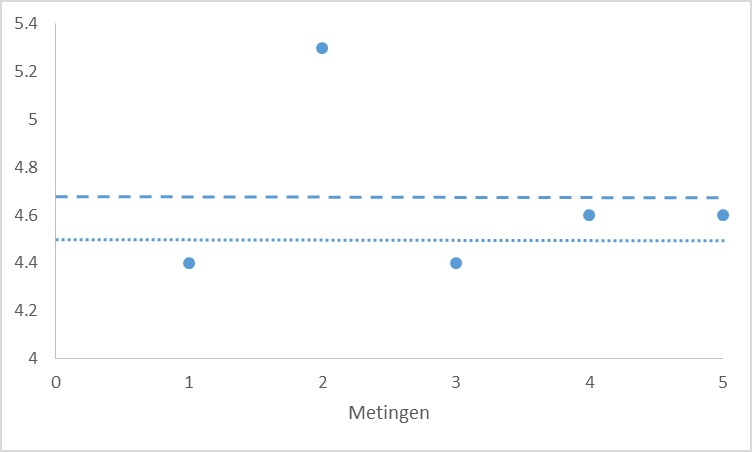
Als je deze waarden gebruikt in je berekeningen vind je een gemiddelde van 4,66. De tweede waarde (5,3) valt echter uit de toon. Zonder deze waarde zou je een ander (en waarschijnlijk beter) gemiddelde vinden. Kijk ook eens naar de metingen die je zelf tijdens de eerste les vaardigheden hebt verricht. Zitten daar ‘verdachte’ waarden tussen?

Soms weet je nog dat er wat mis ging op het lab, en kun je daarom je datapunt met goede reden weggooien. Dat lukt echter lang niet altijd (wel een goede reden om dus altijd echt een goed labjournaal bij te houden!).

Maar je kan een datapunt niet zomaar weggooien omdat hij je niet bevalt. Er is altijd een kans dat de verdachte waarde geen echte outlier is maar werd veroorzaakt door zuiver toeval. Waar trek je de grens, en wanneer noem je iets een outlier? Statistiek kan hierbij helpen: je kunt op basis van een kansberekening gaan kiezen of het datapunt mee mag blijven doen of niet. Een methode hiervoor is de methode van Dixon (ook vaak de Q-test genoemd). Die is geschikt als je weinig datapunten hebt (maximaal 25, meestal bij minder dan 10).

Waarschuwing vooraf: de Q-test kun je niet gebruiken als je:

• maar 1 of 2 datapunten hebt
• maar 3 datapunten hebt, en daarvan zijn er twee precies hetzelfde. Of 4 datapunten en daarvan zijn er 3 precies hetzelfde. etc (dus als n-1 datapunten precies hetzelfde zijn).

Dixons Q-test

De Dixons Q-test is specifiek bedoeld voor de situatie dat je weinig herhaalde metingen hebt, en er is er eentje wel erg vreemd. Dus stel, je meet 5 keer het suikerpercentage van een flesje cola, en een van de 5 metingen is twee keer zo hoog als de andere vier.

Herhaalde metingen zijn meerdere metingen van dezelfde variabele bij hetzelfde flesje cola, hetzelfde pak sinaasappelsap, dezelfde persoon, patient, proefdier etc. Doe je een steekproef met 50 metingen, en is 1 van je metingen wel erg vreemd, dan heb je daar weer andere tests voor. Die behandelen we niet in deze cursus.

Bekijk hier een kennisclip over de Dixons Q-test (let op dat de formule voor Q verschilt per hoeveel metingen (n) je hebt. Check je formulekaart voor de juist formule):

De gegevens voor de Q-test staan op je formuleblad:

1. Pak je formuleblad erbij en ga naar blz 2 (“Kritische waarden voor de Dixon-test voor outliers).
2. Je moet een zgn. \(Q-waarde\) berekenen. De manier waarop deze \(Q\) moet worden berekend is afhankelijk van een aantal meetpunten. De berekening staat als formule in tabel voor de Dixon test voor outliers, in de meest linker kolom. Zo is voor 3 t/m 7 meetpunten de berekening als volgt gedefinieerd (r10 in de de tabel mag je gewoon lezen als ‘Q’):

\(Q=\frac{x2−x1}{xn−x1}\)

De betekenis van de diverse “x-jes” in de formule is als volgt: Je hebt n metingen verricht. In gedachten rangschik je alle metingen op zo’n manier dat je begint met de outlier. Als je een mogelijke outlier naar beneden hebt, begin je dus met de kleinste waarde x1, dan de één na kleinste x2, tot de grootste waarde die dan xn heet. Als je een outlier naar boven wilt testen, stelt x1 de grootste waarde voor, x2 de op één na grootste, en uiteindelijk xn de kleinste waarde.

Exercise 2

De waarden in het grafiekje hierboven waren 4,4; 5,3; 4,4; 4,6 en 4,6 welke is onze verdachte?

hoeveel is N?

Klik hier voor het antwoord

5.3 is de mogelijke outlier, naar boven toe

N is 5 (5 metingen)

Exercise 2

Zet de waarden in volgorde, en vul in:

• x1 =
• x2 =
• x3 =
• x4 =
• x5 =

Reken vervolgens \(Q\) uit met de juiste formule in de tabel op het formuleblad.

Klik hier voor het antwoord

• x1 = 5,3
• x2 = 4,6
• x3 = 4,6
• x4 = 4,4
• x5 = 4,4

\(Q\) = (4,6-5,3) / (4,4-5,3) = 0,778

Stel, we willen die verdachte waarde er graag uit gooien. Dan wil je graag weten hoe groot de kans zou zijn dat je dit punt zou vinden en het is geen outlier. Is die kans nou heel klein, dan kun je hem rustig weg gooien. Meestal spreken we af dat die kans kleiner moet zijn dan 5%, dat heet een significantiewaarde \(\alpha = 0.05\).

In de Q-test hoef je die kans niet zelf uit te rekenen. De waarde die Q moet overstijgen (=de kritische Q-waarde of \(Q_{kritisch}\)) om onder een bepaalde \(\alpha\) te komen staan in de tabel op je formuleblad.

3. Je zoekt \(Q_{kritisch}\) op in de tabel in de juiste kolom en de juiste regel. Kies de kolom voor de \(\alpha\)-waarde die je wilt (meestal 0.05). Kies de regel met het aantal metingen dat je hebt (in dit geval n=5). In de kolom α=0,05 vinden we dan \(Q_{kritisch}=0,642\). Dit is de waarde waar jouw Q-waarde overheen moet om bij een \(\alpha\)-waarde van 0.05 als outlier bestempeld te worden.
4. Vergelijk deze \(Q_{kritisch}\) met jouw berekende \(Q\). Is je berekende \(Q\) groter, dan is het een outlier.

Exercise 2

Was de meetwaarde van 5.3 een outlier bij een \(\alpha\)-waarde van 0.05?

Klik hier voor het antwoord

ja.

\(Q\) = 0,778 \(Q_{kritisch}\)=0,642

0,778 > 0,642, dus het is een outlier

Merk op dat de waarde van \(Q_{kritisch}\) in de tabel toeneemt naarmate α kleiner wordt.

Exercise 2

Was de meetwaarde van 5.3 een outlier bij een \(\alpha\)-waarde van 0.01?

Klik hier voor het antwoord

nee

\(Q\) = 0,778 \(Q_{kritisch}\)=0,780

0,778 < 0,780, dus het is geen outlier

Of je iets een outlier gaat noemen, hangt er dus vanaf met welke betrouwbaarheid je dat wilt doen. Wil je een \(\alpha\)-waarde van 0.05, dan zeggen we ook wel dat je met een betrouwbaarheid van 95% bepaald of iets een outlier is (0.05 is 5%, 100-5 = 95%).

Stappenplan Dixons Q-test

1. wijs je verdachte waarde aan. Dit is \(X1\).
2. controleer of niet al je andere metingen precies gelijk aan elkaar zijn. Is dat het geval (bijvoorbeeld je metingen zijn: 4.1; 4.1; 4.1 en 4.3) dan kun je geen Q-test doen en moet je je verdachte waarde gewoon meenemen.
3. bepaal je aantal metingen \(n\)
4. Zet je waarden in oplopende of aflopende volgorde, te beginnen met verdachte waarde \(X1\). Vind \(X2\) en \(Xn\).
5. zoek de berekening voor \(Q\) op op je formuleblad en bereken \(Q\)
6. Kies een \(alpha\) (meestal 0.05) en zoek de juiste \(Q_{kritisch}\)
7. Kijk of \(Q > Q_{kritisch}\). Ja? dan is het een outlier.
8. Gooi je outlier uit je dataset. Die doet niet meer mee voor verdere berekeningen.
9. Einde. Je mag het niet nog een keer doen met dezelfde dataset.

Opmerkingen Q-test

• Het is hoe dan ook fout een waarde zonder verdere uitleg te negeren! Als je een waarde niet meeneemt in je berekeningen is het belangrijk te vermelden welke waarde dit is en waarom je die waarde niet meeneemt in je berekening (statistische reden, fout of vergissing tijdens experiment, etc.).
• Als je al weet dat je waarde afwijkt omdat je een fout hebt gemaakt op het lab (per ongeluk reagens vergeten toe te voegen of zo), dan hoef je geen Q-test te doen.
• De methode van Dixon werkt alleen maar goed als je te maken hebt met een set metingen waar maar 1 outlier in zit. Als er meerdere outliers in zitten is deze methode te simpel en heb je andere technieken nodig die we hier niet zullen behandelen.
• De methode van Dixon is alleen geldig voor herhaalde metingen van dezelfde waarde.

Oefenen om data te visualiseren aan de hand van een lijngrafiek

In dit experiment wordt de hoeveelheid antioxidant gemeten in een aantal verschillende samples. Van deze data gaan we ook een lijngrafiek maken.

Sample	Wat?
A	Vitamine C tablet (Vitamine C is een bekende antioxidant)
B	Sinaasappelsap uit pak merk 1
C	Sinaasappelsap uit pak merk 2
D	Verse jus 1
E	Verse jus 2

10 μl van de onverdunde samples wordt onder elkaar in een plaat gepipetteerd (rij A-E, kolom 1) en vervolgens 7 keer doorverdund in water (kolom 2-8) met telkens een factor 3. De samples in kolom 8 zijn dus 37 = 2187 keer doorverdund. Alleen in welletje A10 wordt water gepipetteerd zonder verdere toevoegingen. Dit is de blanco meting. Hieronder staat aangegeven per welletje hoeveel elk sample is verdund:

Rij/Kolom	1	2	3	4	5	6	7	8	9	10
A Vitamine C	1	3	9	27	81	243	729	2187		Blanco
B Pak Merk 1	1	3	9	27	81	243	729	2187
C Pak merk 2	1	3	9	27	81	243	729	2187
D Verse jus 1	1	3	9	27	81	243	729	2187
E Verse jus 2	1	3	9	27	81	243	729	2187

In de gevulde welletje van de 96 wells plaat wordt 100 µl DPPH (2,2-Diphenyl-1-picrylhydrazyl) toegevoegd. DPPH is een stof met een vrije radicaal en is met deze vrije radicaal paars van kleur. Het kleurt geel wanneer het geneutraliseerd wordt door anti-oxidanten. Met behulp van een spectrofotometer wordt de kleurintensiteit bij een golflengte van 517 nm (paars) gemeten. Dus: Hoe meer antioxidanten in het welletje, hoe minder paars de kleuring en hoe lager de gemeten extinctie.

Importeren van de data

Voor dit deel van het werkcollege heb je het bestand DataImporteren.txt nodig.

• Open dit bestand in Excel door via File > Open en Browse het bestand op te zoeken.

Omdat het bestand met meetwaardes geen Excel bestand is, is het niet meteen zichtbaar (alleen Excel bestanden worden weergegeven).

• Verander All Excel Files naar All Files
• Selecteer het bestand en druk op Open

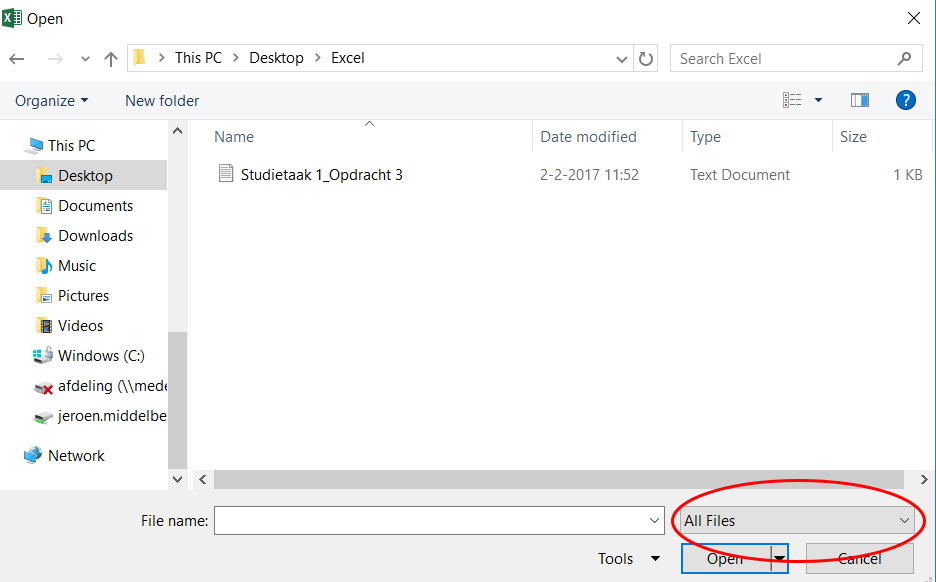
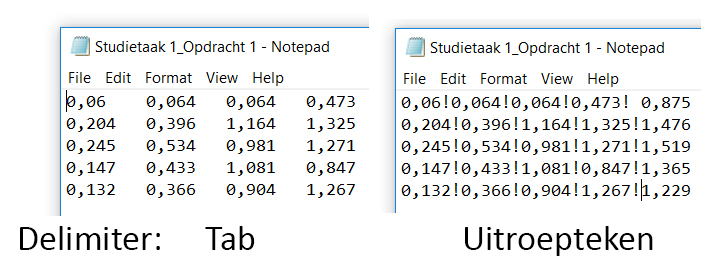
Het bestand wordt herkent als text bestand. Met behulp van de Text Import Wizard kan deze text eenvoudig worden omgezet naar het Excel format. In een text file worden kolommen gescheiden door een ‘delimiter’. Alle leestekens, spaties en tabs kunnen dienen als delimiter:

• Klik in de Text Import Wizard op Next wanneer de optie Delimited is geselecteerd.

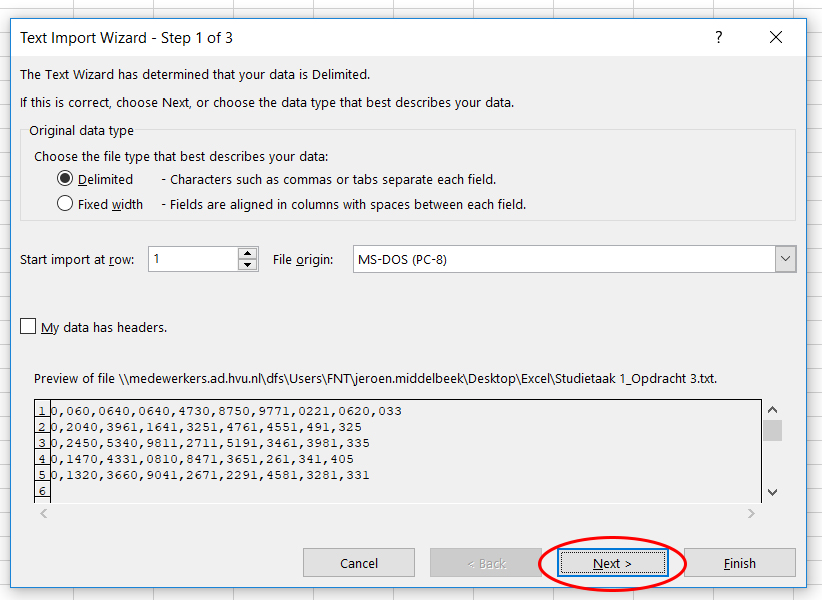
• De data in dit bestand zijn gescheiden door een tab. Vink Tab aan en klik op Next.

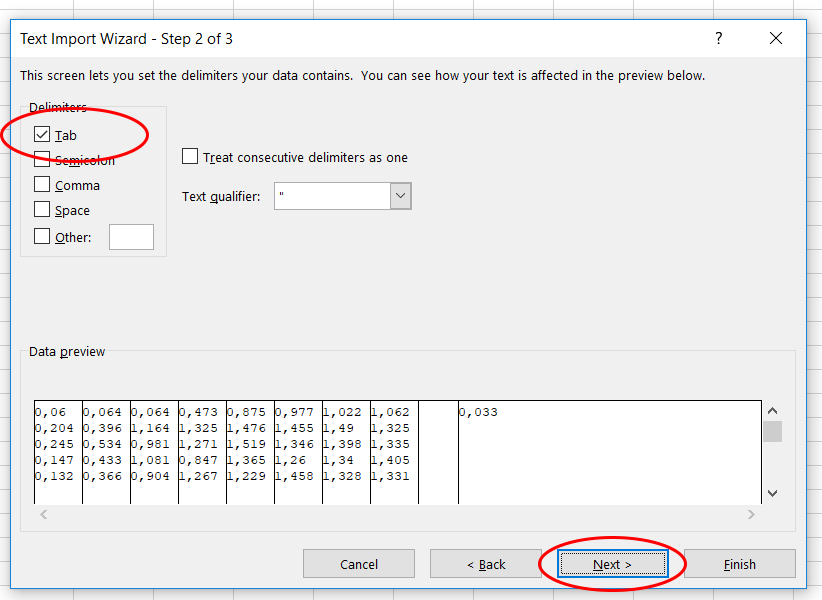
• Klik in het volgende scherm op Finish. De data verschijnt nu in je Excel spreadsheet.

• Sla je spreadsheet op als Excel file. Dit doe je door in het menu File te kiezen voor Save As, het bestand een naam te geven en bij File Type te kiezen voor Excel Workbook. De bestandsnaam krijgt nu een ‘.xlsx’ extentie.

Organiseren van de data

Je gaat nu aangeven wat de verschillende rijen en kolommen zijn. Om ruimte te maken voor de labels, kun je eerst de data als volgt verplaatsen:

• Selecteer de data met je muis van A1:J5. Er zijn verschillende manieren om data te verplaatsen:
  • Ga met de muis naar de groene rand. Er verschijnt een zwart kruisje met pijltjes. Sleep de data zodat de inhoud van A1 terecht komt in B3.
  • OF: Na selectie klik op de rechtermuisknop en selecteer Cut of gebruik de toetsencombinatie ctrl + x. Selecteer nu cel B3 en plak de data door op de rechtermuisknop de drukken en vervolgens Paste te selecteren óf gebruik de toetsencombinatie ctrl + v.

Data zonder labels zijn zinloos. Label daarom altijd je data in Excel!

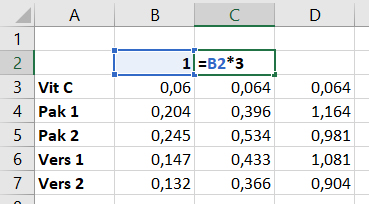
• Voeg in kolom A labels toe zoals aangegeven in het pipeteerschema zodat je weet welke extincties horen bij welke monsters.
• Typ in B2 de verdunningsfactor voor het onverdunde samples (1 staat voor onverdund).

De monsters in kolom C zijn drie keer verdund ten opzichte van de monsters in kolom B. In kolom D zijn de monsters 3 verdund ten opzichte van de monsters in kolom C etc.

• Vul in cel C2 de formule =B2*3.
• Kopieer cel C2 en plak de formule in de cellen D2:I2. In Excel kopieer je altijd de formule (als er een formule in een cel staat) en niet de uitkomst van de formule.
• Label ook de blanco in K3.

De laatste stap in het organiseren van de data is om de data te transponeren. Dit betekent het omdraaien van de rijen en kolommen.

• Selecteer de data zoals aangegeven in de figuur en kopieer de data (ctrl + c).

• Selecteer met de cursor cel A10.
• Druk op de rechter muisknop.
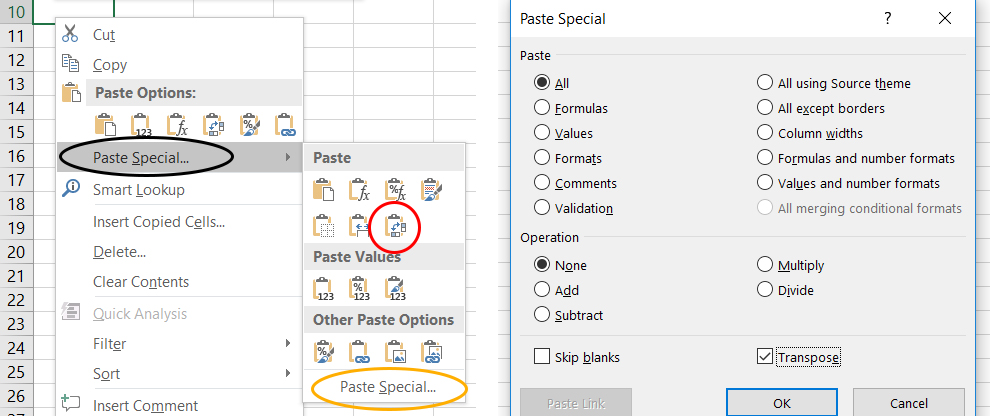
• Ga met de muis naar Paste Special (zwarte cirkel)
• Je kunt op twee verschillende manier de data getransponeerd plakken: * Transponeer de data door op transpose symbool te klikken (rode cirkel). * OF: Klik weer op Paste Special (oranje cirkel). Nu verschijnt het Paste Special venster. Selecteer Values, None and Transpose zoals hieronder aangegeven en klik op OK.

Bewerken van de data

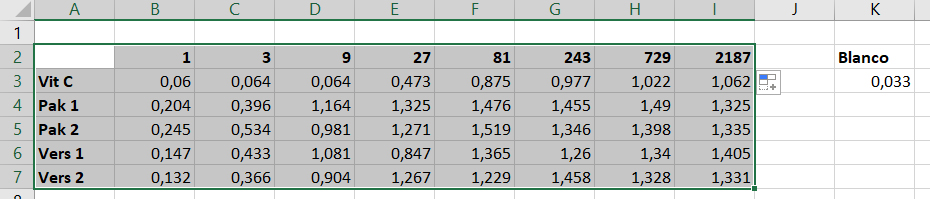
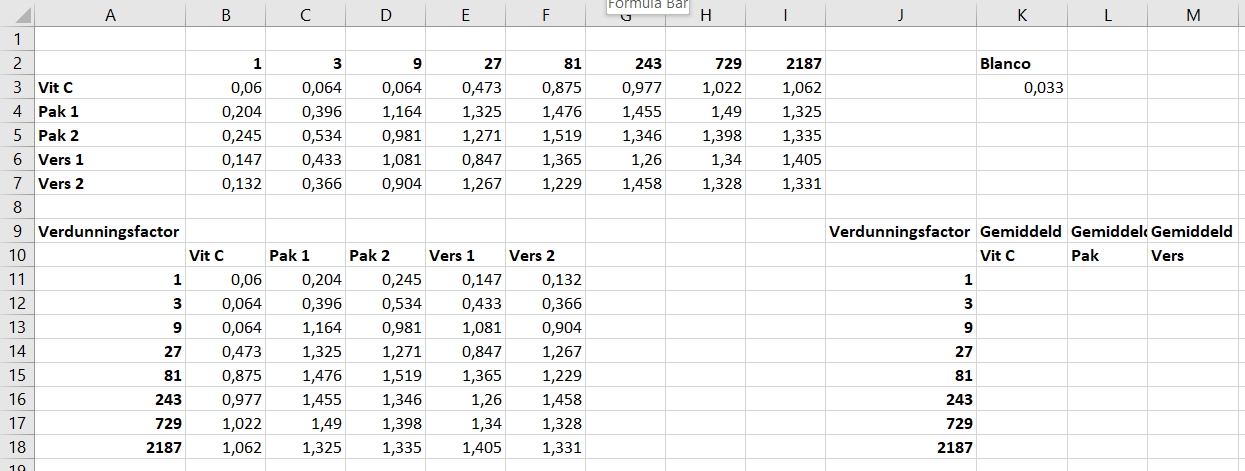
Voordat je begint met de analyse, voeg je nog extra labels toe:

• Schrijf in A9 ‘Verduningsfactor’.
• Kopieer kolom A9:A18 naar J9:J18. Voeg in kolom K, L en M de labels toe zoals aangegeven in onderstaand figuur.

Nu ga je de gemiddelde extinctie per monster uitrekenen in kolom K11:K18, L11:L18 en M11:M18. De extincties van verdunde Vitamine C monsters zijn maar 1 keer gemeten, dus deze waardes kun je direct overnemen uit kolom B.

• Typ in cel K11 =B11 en kopieer K11 naar K12:K18.

De extincties van verdunde sinaasappelsap uit pak en verse jus zijn wel in duplo gemeten.

• Typ in cel L11 =average(C11:D11) en druk op toets Enter. Kopieer cel L11 naar L12:L18.
• Typ in cel M11 =average(E11:F11) en druk op toets Enter. Kopieer cel M11 naar M12:M18.

Vervolgens corrigeer je de gemiddelde meetwaardes voor de blanco meetwaarde. Een blanco meetwaarde is een meetwaarde waarin de reactie NIET heeft plaatsgevonden of waarin de reagentia NIET aanwezig zijn. Dit geeft een achtergrond- of een “baseline” waarde.

• Label cellen RO9:R18 zoals aangegeven in het onderstaande figuur.
• Typ in cel P11 =K11-K3 en druk op de toets Enter.

• Kopieer cel P11 naar P12:P18 en naar Q11:R11.
• Kijk nu goed naar de waardes waar de blanco van is afgetrokken. Bijvoorbeeld vergelijk K12 met P12. Is de blanco waarde eraf? We zien ook ‘#VALUES’ in cel P17 en P18. Het lijkt alsof alleen P11 gecorrigeerd is voor de blanco. Iets klopt er niet!

We gaan uitzoeken wat er niet goed is gegaan.

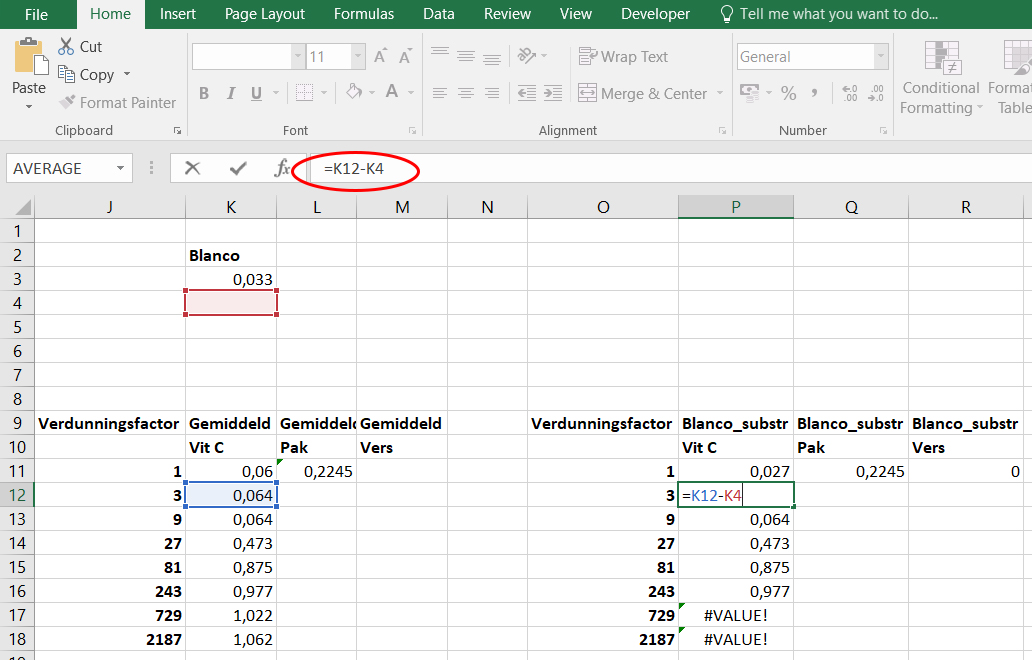
• Ga naar cel P12 en dubbel klik.

Nu zie je de formule en welke cellen gebruikt zijn voor de formule. De formule is ook zichtbaar in het formulevenster (rode cirkel). Wat valt op? In plaats van =K12-K3 staat er nu =K12-K4. De verwijzing naar de blanco waarde is verschoven van K3 naar K4!

• Ga naar cel Q11. Wat valt nu op?

LET OP Als we een formule kopiëren naar beneden/boven, of naar links/rechts dan verschuiven alle cellen waarnaar wordt verwezen ook mee.

De foute formules kun je verbeteren door de verwijzing naar de blanco-waarde in de formules vast te zetten. Dit doe je met een $ teken. De verwijzing naar de blanco-waarde in K3 zet je als volgt vast:

• Verwijder alle verkeerde formules.
• Ga naar cel P11 en dubbel klik. Je kan ook direct naar het formulevenster gaan en daar je cursor plaatsen.
• Plaats een $ teken voor de K om de verwijzing naar kolom K vast te zetten, en plaats het $ teken voor de 3 en druk op de toets Enter.
• Kopieer de nieuwe formule in alle cellen van Vit C (P12:P18), Pak (Q11:Q18) en Vers (R11:R18).
• Dubbel klik een willekeurige cel in het bereik van P11:R18 en controleer of de formule nu wel goed is.

LET OP Het kan ook voorkomen dat je alleen de verwijzing naar de kolom (in dit voorbeeld $K3) of alleen de rij (K$3) wilt fixeren.

Data uitzetten in een grafiek

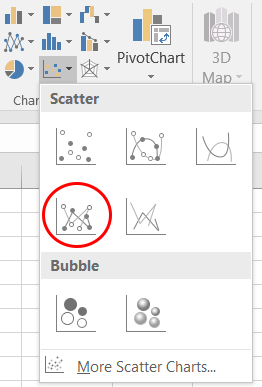
Je gaat nu de dataset uitzetten in een grafiek.

• Voeg een scatter plot in zoals je dat hebt geleerd in de vorige les. Kies nu voor grafiektype Scatter with straight lines and markers.

• Voeg de waardes voor Vit C, Pak en Vers in als afzonderlijke series.
• Selecteer voor iedere serie de verdunningsfactor als x-waardes en de bijbehorende gecorrigeerde gemiddelde extincties als y-waardes.

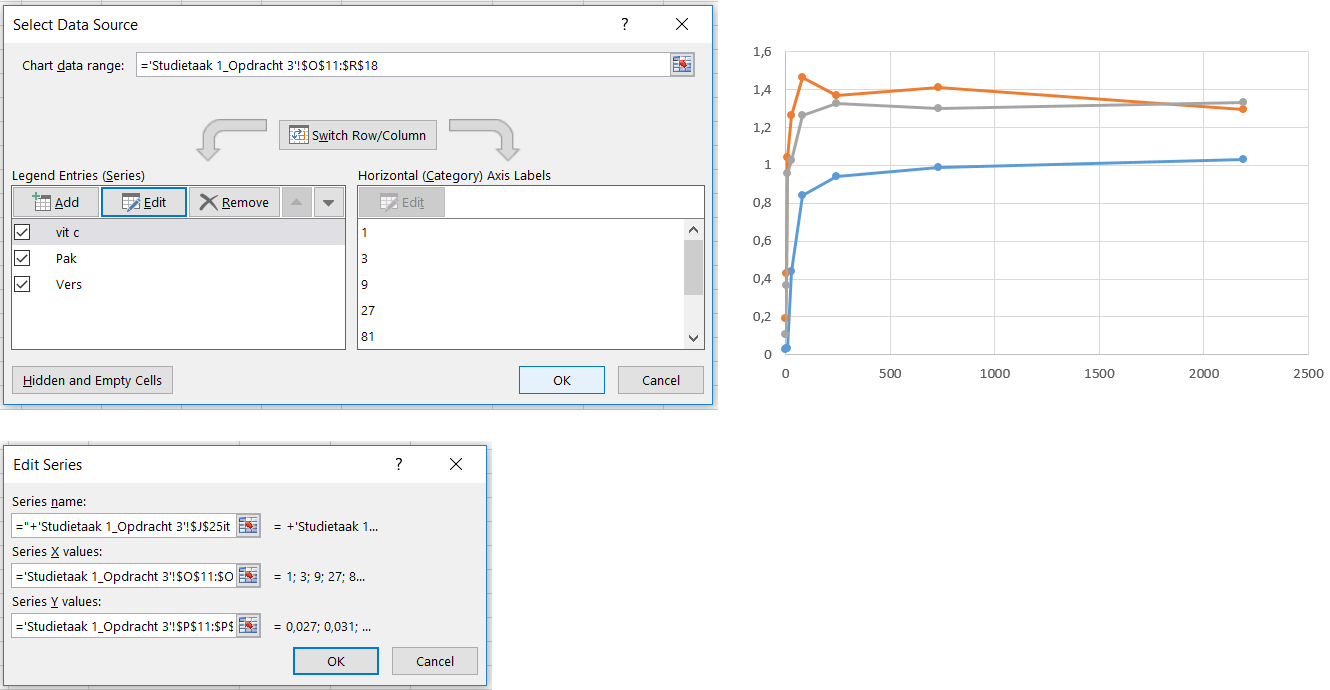
In deze grafiek zijn de meeste datapunten verzameld tussen x-waarden 0 en 100. Waarom zijn de datapunten zo scheef verdeeld? Hoe kunnen we dit corrigeren?

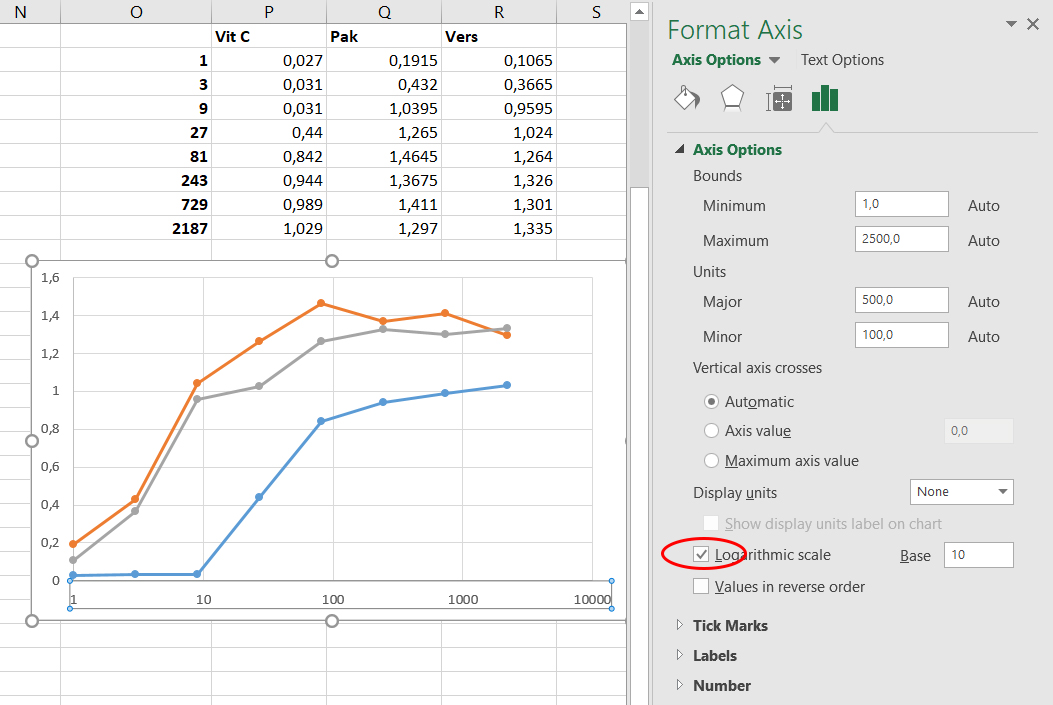
De monsters zijn serieel verdund: In elk van de 7 opeenvolgende verdunningsstappen werd het monster 3 keer verdund. Elke stap op de x-as vertegenwoordigd dus een 3-voudige verdunning t.o.v de vorige stap. De verdeling van de meetpunten op de x-as is niet lineair terwijl de indeling van de x-as dat wel is! Door een logaritmische schaal verdeling te gebruiken op de x-as verdeel je de meetpunten wel gelijk over de x-as.

• Dubbel klik op de op de x-as (of een waarde van de x-as). Rechts in je werkblad verschijnt een nieuw panel Format Axis.
• Vink de Logaritmic scale optie aan.

De grafiek is nog niet af. Je mist nog duidelijke labels bij de x-as en y-as labels, én een grafiektitel.

• Klik op de grafiek en klik op de het groene + teken aan de rechterzijde van de grafiek. Een lijst met Chart Elements verschijnt.
• Vink de Axis Titles optie aan. Een x-as en y-as titelvierkant verschijnt. Voeg hier tekst toe.
• Vink de Chart Title optie aan. Voeg de grafiektitel toe.
• Klik op Legend en rechts op het kleine grijze pijltje. Selecteer de optie Right om de legenda aan de rechterkant te laten verschijnen.

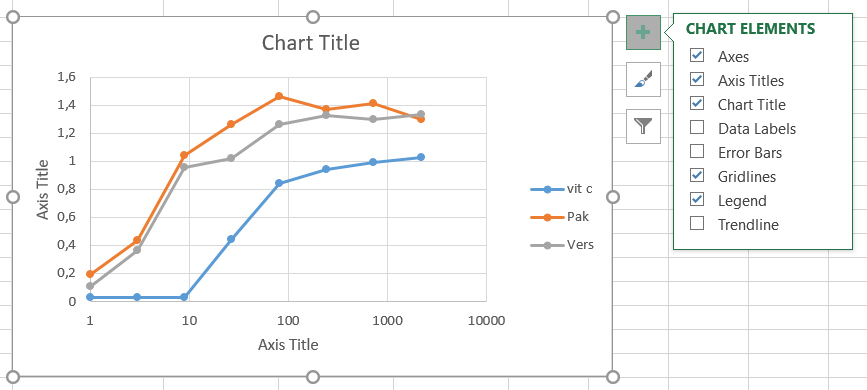
Het is erg belangrijk om een complete grafiek te maken met duidelijke labels. De lezer moet een grafiek kunnen begrijpen zonder extra uitleg of tekst.

In het algemeen, als je een element van een grafiek wilt veranderen, dubbelklik op het element en aan de rechter zijde verschijnt een nieuw venster met allerlei opties. Een alternatieve manier is om het element aan te klikken en vervolgens klik je op de rechtermuisknop. Selecteer een format optie in het popdown menu en rechts verschijnt weer een nieuw venster met allerlei opties.

Exercise 2

Leidt een lage concentratie anti-oxidant tot een hoog of een laag aantal vrije radicalen in de stof DPHH?

Klik hier voor het antwoord

Tot een hoog aantal vrije radicalen.

Exercise 2

Leidt een hoge concentratie anti-oxidant tot een hoog of een laag aantal vrije radicalen in de stof DPHH?

Klik hier voor het antwoord

Tot een laag aantal vrije radicalen.

Exercise 2

Welk monster heeft de hoogste anti-oxidant activiteit?

Klik hier voor het antwoord

Verse sinaasappelsap.

Exercise 2

Waarom zijn de extincties van Vitamine C het laagst?

Klik hier voor het antwoord

Vitamine C is de positieve controle voor de omzetting van DPHH. De hoeveelheid anti-oxidant in de positieve controle is dus hoger.

Exercise 2

Bij welke verdunning van Vitamine C raakt de omzetting van DPHH verzadigd?

Klik hier voor het antwoord

Bij de 10x verdunning.

Werkcollege casus visualiseren

Glucose concentratie bepalen met een kalibratielijn

Maak op basis van de onderstaande data een kalibratielijn. Deze data komt overeen met de situatie beschreven in de voorbereidingen; we meten de glucose concentratie van een bloed sample op basis van een kleuromslag. Zorg ervoor dat de grafiek voldoet aan de algemene regels van het grafiek format. Kies een willekeurig exinctie punt en bereken de corresponderende concentratie en visualiseer dit in je grafiek.

Table 7: Extinctie data van glucose verdunningen voor kalibratielijn.

A	B	C	D
Concentratie mmol/L	Extinctie 1	Extinctie 2	Extinctie 3
20	1.532	1.432	1.632
6.67	0.683	0.583	0.783
2.22	0.324	0.324	0.314
0.74	0.227	0.227	0.247
0.08	0.102	0.122	0.102