4: Variatie

Lesinhoud en leerdoelen

Tijdens deze les maak je kennis met enkele basisbegrippen en concepten in dataverwerking. In een biomedisch laboratorium zal je regelmatig (kwantitatieve en kwalitatieve) metingen verrichten. Het is belangrijk om je daarbij bewust te zijn van mogelijke meetfouten en andere variatie in je data en de effecten daarvan op je conclusies. Je leert in deze les ook de nauwkeurigheid van gemeten kwantitatieve waarden op een juiste manier afronden en noteren.

Aan het einde van deze les kun je:

uitleggen welke verschillende soorten fouten en foutoorzaken er bij het meten bestaan;
aangeven wat het effect van toevallige variatie is op een meting;
uitleggen wat de normaalverdeling is;

Theorie:

meetfouten
biologische variatie
de normaalverdeling
spreiding: de standaarddeviatie

Vaardigheden:

meetwaarden met meetfouten afronden
error bars toevoegen aan grafieken in Excel
beschrijvende statistiek: gemiddelde en standaarddeviatie samen beschrijven
een staafdiagram maken
een boxplot maken
populatiegemiddelde schatten: het 95% betrouwbaarheidsinterval berekenen

Voorbereiding

Steekproeven

Data verzamel je over het algemeen om een antwoord te geven op een vraag: een onderzoeksvraag. Die zijn vrij specifiek. “Hoe zit het eigenlijk met konijnenoren?” is een vraag, maar “Zijn konijnenoren op de Uithof langer dan die van het gemiddelde konijn?” is een onderzoeksvraag: je kan een onderzoek doen om een antwoord te vinden op je vraag.

De onderzoeksvraag bepaalt dus ook voor een deel wat voor onderzoek of experiment je zou kunnen doen! Vergelijk bijvoorbeeld (en er zijn veel meer voorbeelden denkbaar):

“Eten de studenten in groep VL1205 per jaar meer sinaasappels dan die in VL1206?” : je moet iedereen in VL1205 en VL1206 zo gek krijgen om het hele jaar al hun sinaasappels te tellen.
“Hebben inwoners van Utrecht meer ijzer in hun bloed dan gemiddeld in Nederland?” : je hebt bloed-ijzerconcentraties nodig van inwoners van Utrecht, en een referentiewaarde: de gemiddelde ijzerconcentratie in Nederland (een nummertje, vast op te vragen bij Sanquin of het CBS).
“Hebben inwoners van Utrecht meer ijzer in hun bloed dan inwoners van Groningen?” : je hebt bloed-ijzerconcentraties nodig van inwoners van Utrecht, maar ook van inwoners van Groningen.
“Hebben mensen die meer sinaasappels eten minder ijzer in hun bloed?”: Je hebt van dezelfde mensen data nodig over hun bloed-ijzerconcentratie en over de hoeveelheid sinaasappels die ze eten.

Heel soms kun je de hele populatie meten, dat betekent: alle units (individuen / konijnen / flesjes cola / etc) waar je een vraag over hebt gaat meten. Bijvoorbeeld als alle studenten in VL1205 en VL1206 uit het eerste voorbeeld hierboven wel bereid zijn om sinaasappels te tellen.

Bij de andere voorbeelden is het echter al snel duidelijk dat het niet haalbaar gaat zijn om de hele populatie inwoners van Utrecht op te roepen voor een bloedonderzoekje. Dat gaat ’m niet worden. Toch gaat je onderzoeksvraag over alle Utrechters: over de populatie. Maar hoe komen we dan achter de ijzerconcentratie van Utrechters?

Oplossing: we doen een steekproef. Bij een steekproef meet je niet de hele populatie, maar een deel ervan. Een steekproef moet representatief zijn voor de populatie en wordt gebruikt om voorspellingen te doen over de gehele populatie. Het aantal objecten (elementen) in een steekproef wordt weergegeven met n. Dus meet je 50 Utrechters, dan zeg je: n = 50.

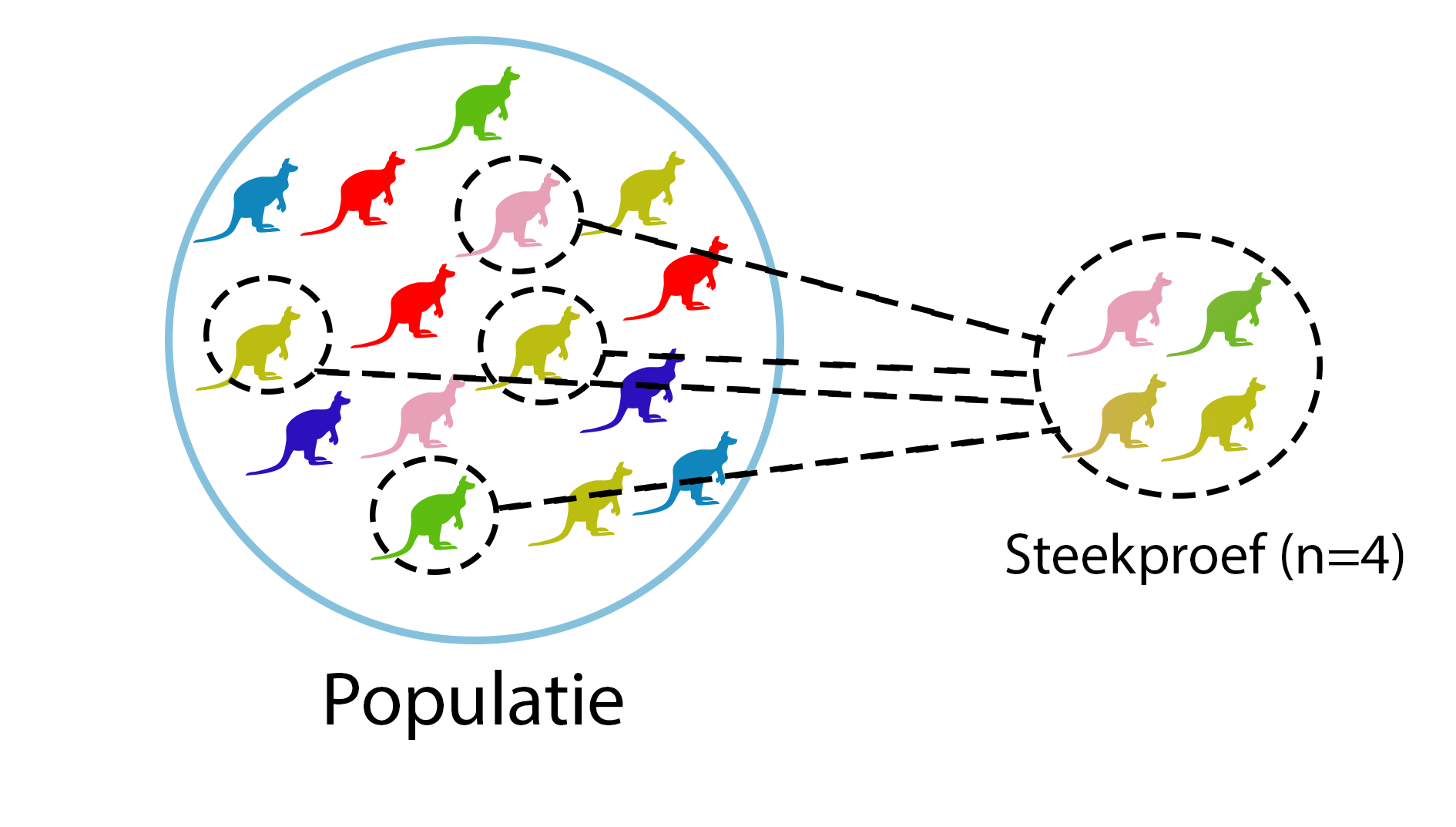
Figure 42: Een steekproef van 4 kangaroes uit een totale populatie van 15

Representatief betekent dat de steekproef ongeveer dezelfde samenstelling heeft als de hele populatie, maar dan in het klein. Dus als je bloed-ijzergehalte in Utrecht onderzoekt, moet je random (=willekeurige) mensen in Utrecht gaan vragen of je hun bloedijzergehalte mag meten, en niet alleen studenten op de Uithof. En ook niet alleen de mensen die sowieso naar de dokter gingen om ijzer te laten testen, want die zitten wellicht wat lager dan de meeste Utrechters…

Inductieve en beschrijvende statistiek

Als je een steekproef doet, heb je niet de hele populatie gemeten. En elke steekproef gaat dus andere data opleveren. Maar je vraag ging over de populatie! Hoe kun je dan toch iets zeggen over die populatie? Dus in het plaatje hierboven: kun je op basis van die 4 kangaroes iets zeggen over de kleuren in de hele populatie? En hoe betrouwbaar is die inschatting? Hiervoor gebruik je inductieve statistiek: de bewerking van data uit een steekproef om een uitspraak te doen over een eigenschap van een populatie. Dit is waar mensen aan denken bij het woord “statistiek”. In deze cursus doen we bijna nog geen inductieve statistiek.

Een andere tak van statistiek is beschrijvende statistiek: Beschrijvende statistiek is de term die wordt gegeven aan de analyse van gegevens waarmee gegevens op een zinvolle manier kunnen worden beschreven, weergegeven of samengevat. Denk bijvoorbeeld aan het beschrijven van de staartlengte van 20 Utrechtse katten met een gemiddelde. Het CBS is bekend om de grote hoeveelheid beschrijvende statistiek.

Beschrijvende statistiek heeft altijd betrekking op de werkelijk gemeten waardes en kan niet gebruikt worden om hypotheses te testen of om een uitspraak te doen over de populatie aan de hand van een steekproef. Daar gaan we nog uitgebreid op in in jaar 2. Beschrijvende statistiek laat het niet toe om conclusies te trekken die verder gaan dan de gegevens die we hebben geanalyseerd. Dan zou je namelijk inductieve statistiek aan het doen zijn. Ze zijn gewoon een manier om gegevens te beschrijven over de populatie (alleen als je de hele populatie gemeten hebt) of de steekproef.

Meerdere steekproeven uit dezelfde populatie

Maar… Al die Utrechters hebben andere bloed-ijzerwaarden. Dus als je een steekproef doet van 100 random mensen, krijg je andere bloedijzerwaarden dan als je nog een keer een steekproef doet van 100 random mensen.

Of in het plaatje hierboven (figuur 42): Nu zijn de 4 kangaroes in de steekproef roze, geel, geel en groen. Maar als je nog een keer 4 random kangaroes uit de populatie kiest zijn ze waarschijnlijk andere kleuren. Het is dus bijna zeker zo dat als je verschillende steekproeven uit 1 populatie neemt, de data wel wat verschillend is. Onthou dit! Als je dat vergeet kan statistiek verderop verwarrend worden.

Biologische variatie

Waar komen die verschillen in data dan vandaan? 1 oorzaak was al duidelijk in het kangaroe-plaatje. Niet alle kangaroes hebben dezelfde kleur, en toevallig kan je bij een steekproef net wel of net geen roze ertussen hebben.

Wanneer je bij verschillende mensen de temperatuur exact zou kunnen bepalen, zal je bij de ene persoon 36,5 graden meten en bij de andere 37,5 graden. Oftewel, we zeggen wel dat mensen een lichaamstemperatuur hebben van 37 graden, maar in werkelijkheid is die lichaamstemperatuur gemiddeld 37 graden, maar varieren mensen pak ’m beet tussen de 36.5 en 37.5 graden.

Dat niet alle kangaroes exact dezelfde kleur hebben, of alle mensen exact dezelfde temperatuur, of niet alle katten exact dezelfde staartlengte, heet biologische variatie.

Meetfouten

De perfecte meting bestaat niet. Wanneer we de temperatuur van een vloeistof meten, zal de gemeten waarde altijd (een klein beetje) afwijken van de werkelijke (populatie) temperatuur. Met andere woorden, we kunnen de werkelijke temperatuur alleen maar gaan schatten door te meten. Deze onnauwkeurigheid komt voort uit zogenaamde meetfouten. We onderscheiden drie type meetfouten: toevallige fouten, systematische fouten en vermijdbare fouten.

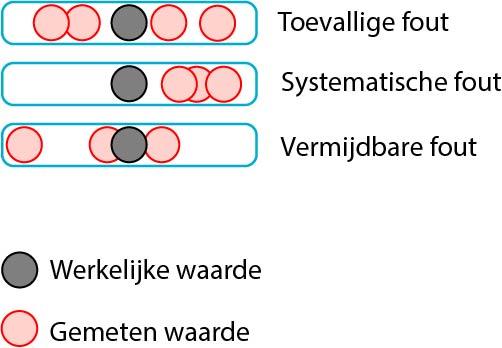
Toevallige fouten

Toevallige fouten zijn altijd aanwezig; ze zijn niet te vermijden. (Ze zijn in die zin dus ook niet “fout”, zo heten ze alleen. Statistici houden er van om dingen namen te geven die niet zo handig zijn in een andere context!) Toevallige fouten zijn het gevolg van twee dingen die te maken hebben met je meting:

Bij het aflezen van de apparatuur. Wanneer je een analoge thermometer afleest zal je moeilijk onderscheid kunnen maken tussen 37,2 en 37,3 graden.
Beperkte gevoeligheid van de meetapparatuur. Een goedkope thermometer kan onderscheid maken tussen 37 en 38 graden, maar niet tussen 37 en 37,2 graden.

Het gevolg van toevallige meetfouten is dat de gemeten waarde soms hoger en soms lager is dan de werkelijke waarde (zie ook bovenstaande figuur). Je kunt daarom de toevallige meetfout eenvoudig verkleinen door vaker te meten en over de gemeten waarden het gemiddelde te berekenen.

Soms wordt biologische variatie ook onder “toevallig fouten” gerekend, omdat het ook een random variatie in je data geeft.

Gevoeligheid van meetapparatuur en significante cijfers

Bij chemisch rekenen (en ook vaak op de HAVO) leren jullie over significante cijfers. Hoe weten we nou op hoeveel significante cijfers je een meetwaarde op zou moeten schrijven? Dat hangt dus af van je meetapparatuur.

Een weegschaal. Ter illustratie. M.Minderhoud, [CC BY-SA 3.0](http://creativecommons.org/licenses/by-sa/3.0/), via Wikimedia Commons

Figure 43: Een weegschaal. Ter illustratie. M.Minderhoud, CC BY-SA 3.0, via Wikimedia Commons

Stel je wilt muizen wegen, en je hebt een weegschaal met streepjes om de 10 gram. Je zet een muis op de weegschaal, en je leest af: het wijzertje op de weegschaal zit ergens tussen de 10 en de 20 gram, beetje dichter bij de 20. Dan kun je dus niet 18.54 gram opschrijven met 4 significante cijfers, want zo precies weet je het gewoon niet.

Systematische fouten

Toevallige fouten geven geen bias. systematische fouten doen dat wel.

Systematische fouten geven een consequente overschatting of juist een onderschatting (maar steeds hetzelfde, daarom heet het “systematisch”) van de werkelijke waarden. Er zijn verschillende oorzaken van systematische fouten:

Wanneer je de lengte van proefpersonen meet terwijl ze nog schoenen dragen, zal je consequent de lengte van deze proefpersonen overschatten.
Het gevolg zijn van verkeerde kalibratie van je apparatuur, verouderde materialen en oplossingen.

Systematische fouten leiden tot vertekening van de resultaten (bias) ten opzichte van de werkelijkheid. Maar ja, die werkelijkheid weten we natuurlijk niet. Systematische fouten zijn daarom erg moeilijk om te herkennen en op te sporen. Maar wanneer de oorzaak en de afwijking bekend is kunnen we er wel gemakkelijk voor corrigeren. Als je wéét dat je weegschaal 10% te zwaar meet, kun je van al je metingen 10% aftrekken.

Vermijdbare fouten

Vermijdbare fouten zijn echte fouten of blunders. Een thermometer geeft bijvoorbeeld aan dat de lichaamstemperatuur 37,5 graad is, maar we noteren 36,5 graad. Ook kan het gebeuren dat een thermometer de temperatuur kan meten in graden Celsius én in Fahrenheit, en we per abuis de temperatuur aflezen in graden Fahrenheit terwijl we denken te meten in graden Celsius. Ook het gebruiken van een verkeerd reagens of het gebruiken van een verkeerde voorschrift zijn voorbeelden van vermijdbare fouten. Vermijdbare fouten leiden tot uitschieters. Gelukkig zie je meestal aan de uitkomst al dat er iets fout is gegaan en is dit soort fouten snel op te sporen.

Exercise 4

Jeroen maakt een bufferoplossing op het lab. In plaats van pH=7,4 schrijft hij pH=7,04 op de fles. Wat voor een fout is dit?

Klik hier voor het antwoord

Een vermijdbare fout.

Exercise 4

De balans van het laboratorium is al twee jaar niet gekalibreerd. Hier door geeft de balans een 5% hogere waarde. Wat voor fout is dit?

Klik hier voor het antwoord

Een systematische fout.

Exercise 4

Om de antistof concentratie in een patiëntenmonster te bepalen heeft Daniël een aantal standaardoplossingen gemaakt voor de ijklijn. Achteraf is gebleken dat bij het verdunnen van de monsteroplossing een P200 volumepipet is gebruikt is in plaats van een P20 pipet. Van welk soort fout is hier sprake?

Klik hier voor het antwoord

Een vermijdbare fout.

Exercise 4

Leonie wil de concentratie van glucose bepalen met een spectrofotometer en heeft daarvoor volgens een bestaand protocol de oplossingen gemaakt. Tijdens de meting van 5 gelijke monsteroplossingen ziet zij echter verschillende absorptie-waarden, die liggen tussen 0,356 en 0,365. Van welk soort fout is hier sprake?

Klik hier voor het antwoord

Een toevallige fout.

Biologische variatie

Als gevolg van biologische variatie is niemand even lang. Stel dat je wilt weten wat de gemiddelde lengte van de hedendaagse Nederlandse man is, en hoe groot de kans is dat een willekeurig individu veel groter of veel kleiner is dan dit gemiddelde, hoe pak je dat aan? De doelgroep waarover je iets wilt weten, alle Nederlandse mannen, wordt in de statistiek de populatie genoemd.

Wanneer de lengte van alle Nederlandse mannen bekend is, dan tel je het aantal individuen met een lengte in een bepaald bereik. Het aantal individuen per interval zetten we vervolgens uit in een histogram (zie grijze staven in de onderstaande grafiek). In de onderstaande grafiek is dat bereik verdeeld in intervallen van 2cm. Uit dit histogram blijkt dat relatief veel Nederlandse mannen een lengte hebben van rond de 1,75 meter, en dat er, naarmate de lengte naar boven of naar beneden meer afwijkt van dit gemiddelde, steeds minder mannen zijn met die lengte. Er zijn dus meer Nederlandse mannen met een lengte van 1,75 meter dan mannen met een lengte van 1,45 meter en 2,09 meter.

In dit voorbeeld gaan we er even vanuit dat A) we alle Nederlandse mannen opgementen hebben (niet zo realistisch) en B) dat je mensen uberhaupt zo makkelijk kan indelen in “wel man / niet man” (ook niet zo realistisch). Maar voor het voorbeeld wel even duidelijk.

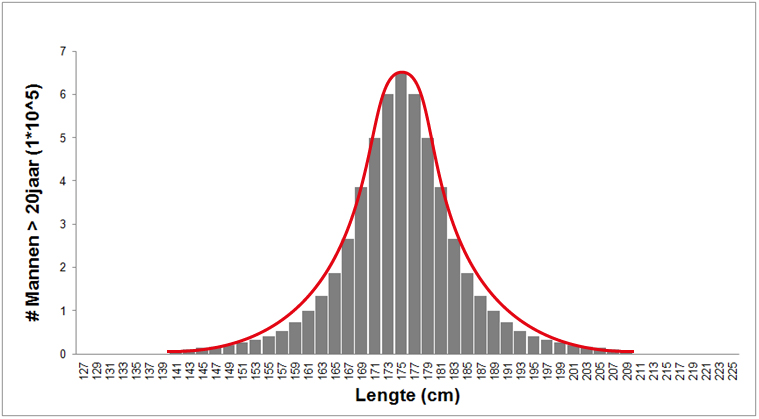
Normaalverdeling

Een karakteristieke eigenschap van biologische variatie is dat de verdeling van waarden om het gemiddelde symmetrisch is. Er zijn dus ongeveer evenveel mannen 10 cm groter dan het gemiddelde als mannen 10 cm kleiner dan het gemiddelde. Deze verdeling van waarden om het gemiddelde heet een normaalverdeling. Als je data in een histogram zet en het lijkt op deze normaalverdeling, dan noemen we dat normaal verdeelde data.

Wanneer we dan alle waarden verbinden door een continue lijn, ontstaat de normaalcurve (zie de rode lijn in het bovenstaande figuur) die wiskundig kan worden omschreven met de volgende functie (die je niet uit je hoofd hoeft te leren):

$f(x)=\frac{1}{σ\sqrt{2π}}e^{-\frac{1}{2}}(\frac{x-\mu}{\sigma})^2$

Bovenstaande formule is bedacht door Carl Friedrich Gauss (1777-1855) met als doel de normale verdeling zoals die in de natuur voorkomt wiskundig te beschrijven. Er wordt daarom ook wel gesproken over een Gauss-curve. De formule lijkt ingewikkeld, maar omdat π en e beide natuurlijke constanten zijn, wordt de vorm van de curve alleen bepaald door (wel belangrijk om te onthouden):

Andere verdelingen

De normaalverdeling is ons lievelingetje, maar er zijn natuurlijk veel andere verdelingen.

Normaalverdeling

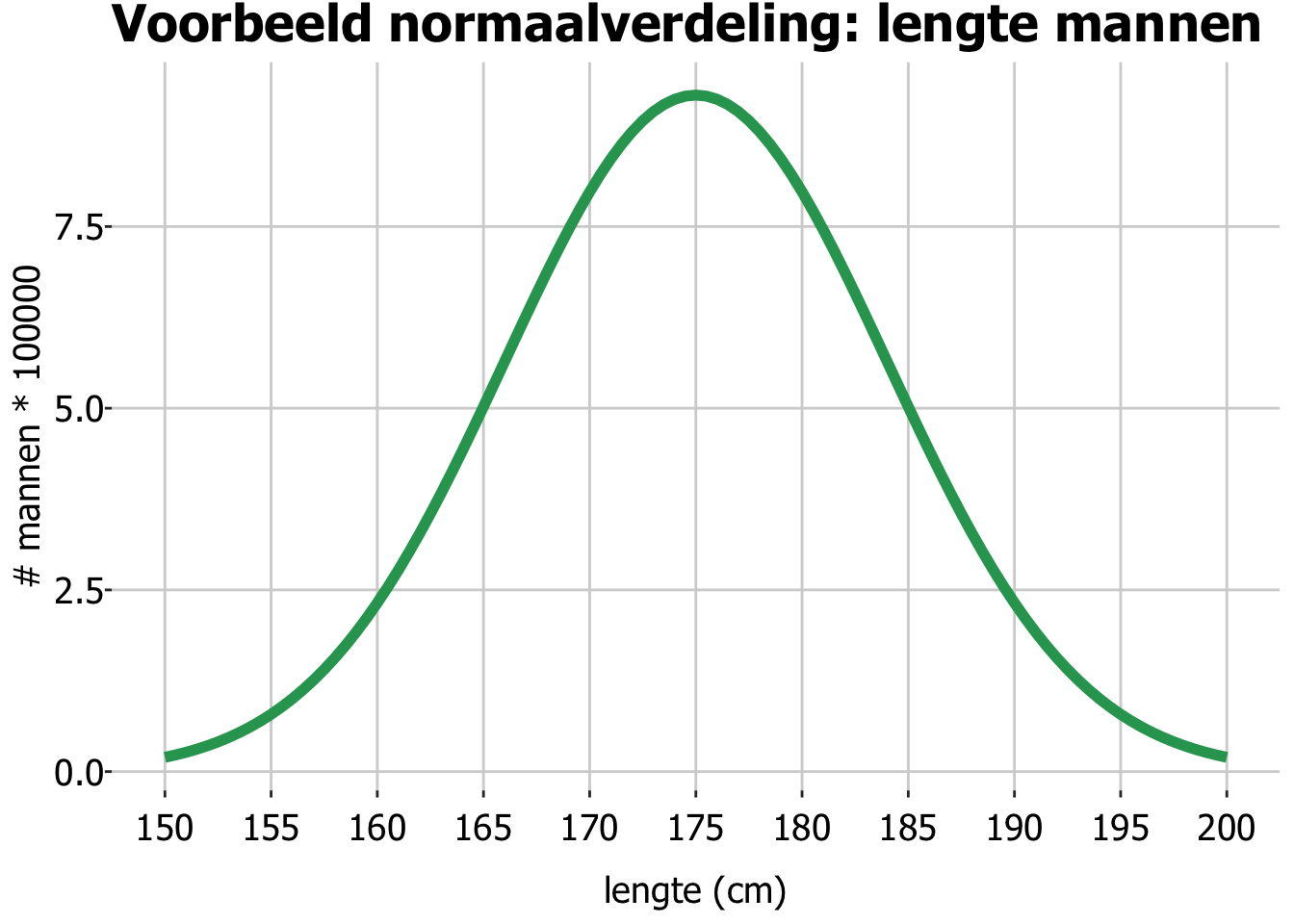
in de normaalverdeling, zijn meetwaarden rond het gemiddelde het meest waarschijnlijk, en een waarde -zeg- 5 eenheden boven het gemiddelde is even waarschijnlijk als een waarde 5 eenheden onder het gemiddelde. Oftewel: de normaalverdeling is symmetrisch.

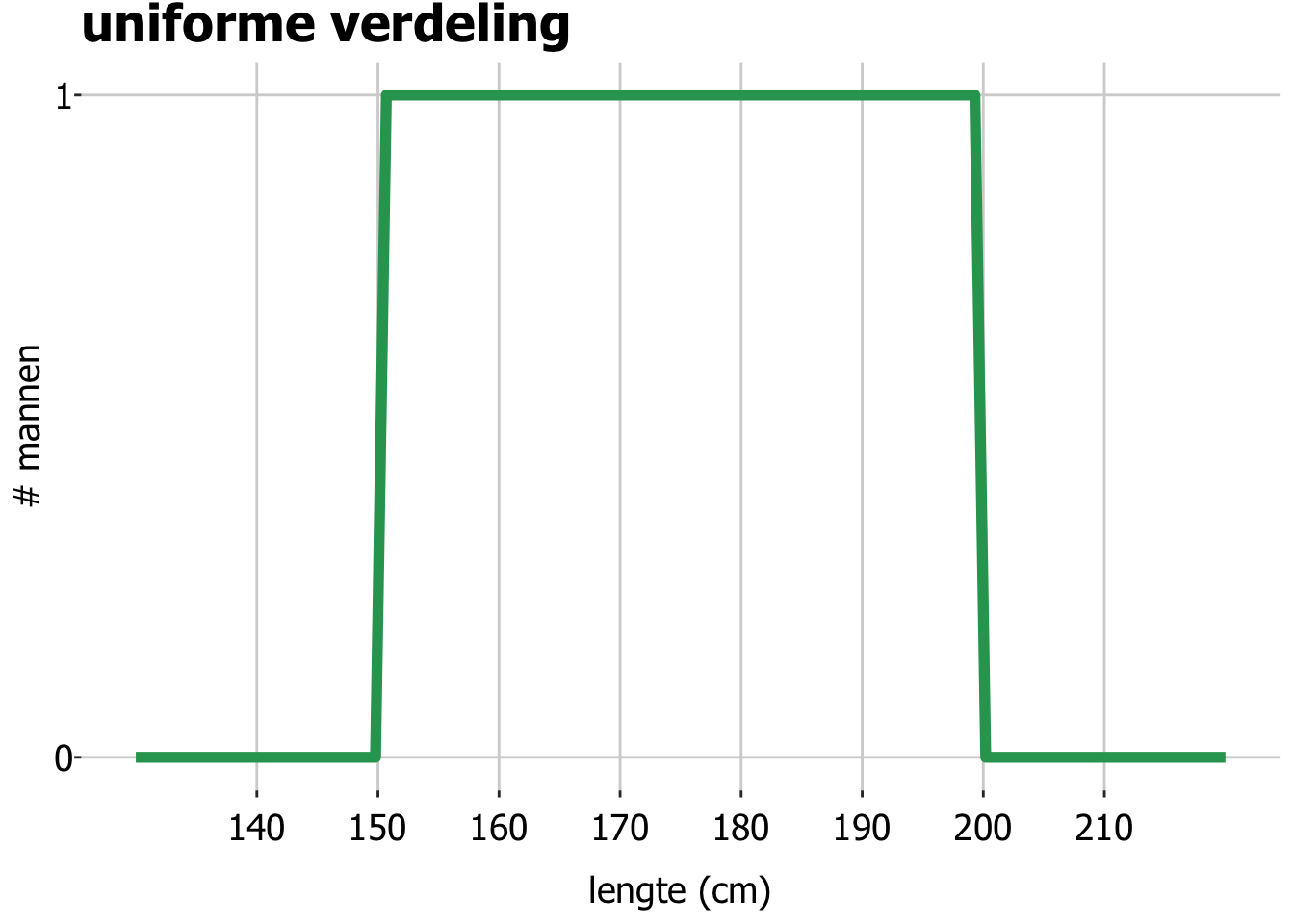
Uniforme verdeling

Stel je nu voor dat we 50 mannen hebben gezocht, voor elke cm tussen 150 en 200 cm lengte precies 1 man met die lengte. Dus 1 man met een lengte tussen de 150 en de 151 cm, 1 man met een lengte tussen de 151 en 152 cm, etc. Hoe beschrijf je deze groep mannen met een functie? Die functie ziet er zo uit, alle lengtes tussen 150 en 200 cm komen even vaak voor:

Poissonverdeling: voor teldata

Hierboven hadden we continue data. Een continue variabele zoals lichaamslengte kan (binnen bepaalde grenzen) iedere waarde aannemen, niet alleen hele centimeters.

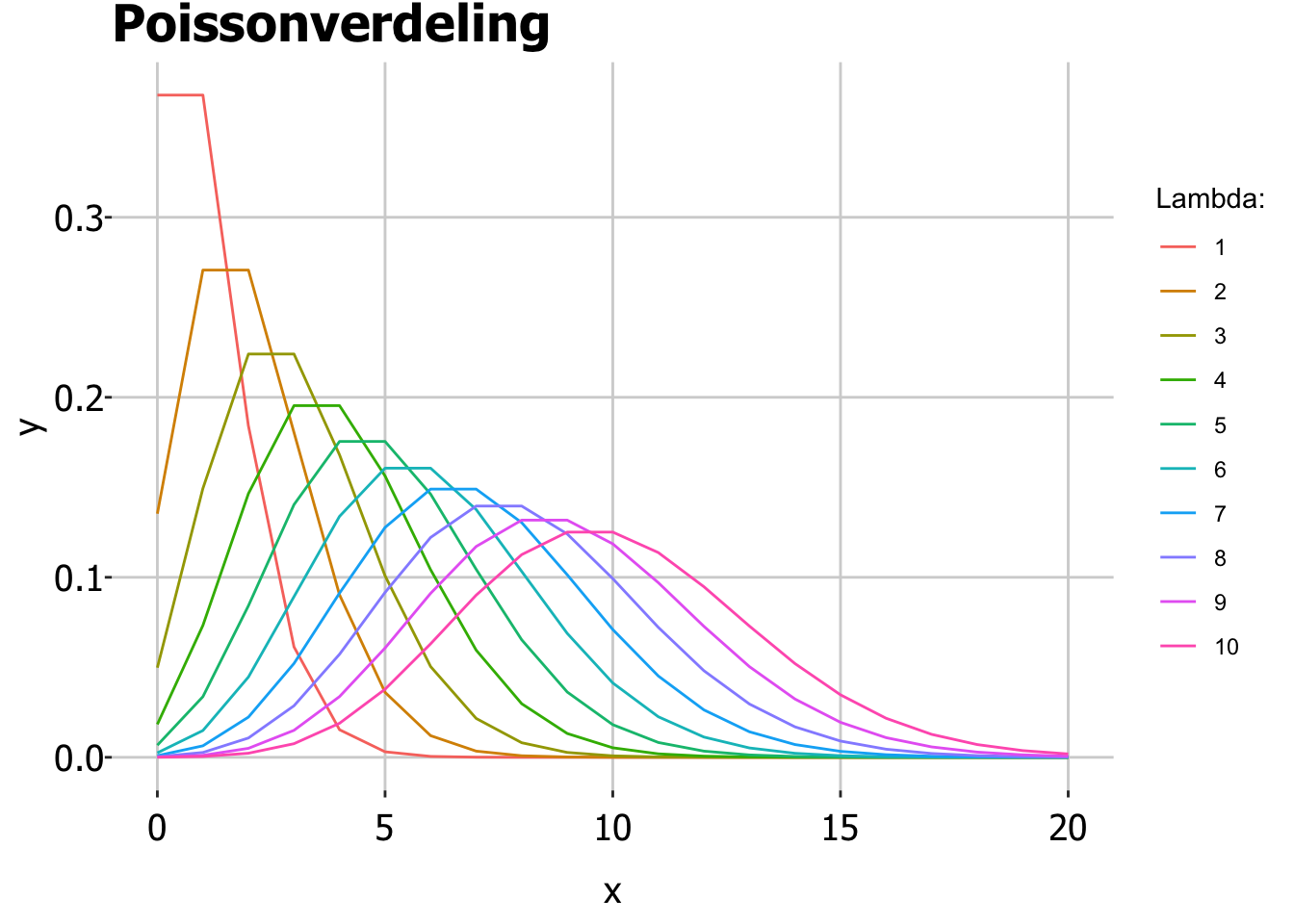
Als je niet aan het meten bent, maar aan het tellen, gebruik je een andere kansverdeling. De Poissonverdeling (uitgevonden door Siméon Poisson) gebruik je als je het aantal van iets per tijdseenheid/oppervlakte/afstand/volume etc aan het tellen bent. Bijvoorbeeld:

het aantal vissen dat per dag door de sluis in Utrecht zwemt
het aantal bomen in de berm per hectometer singel
het aantal rodebloedcellen per microliter bloed (onthoud die, die komt in een later vak dit jaar terug)
het aantal konijnen per vierkante kilometer op de uithof

Deze verdeling wordt alleen bepaald door 1 parameter $\lambda$ (bijv: het verwachte aantal vissen per uur), in tegenstelling tot de normaalverdeling die twee parameters had (gemiddelde en standaarddeviatie).

Bereken je de standaarddeviatie, dan gaat dit dus ook anders dan bij de normaalverdeling. Bij de normaalverdeling hing de standaarddevaitie af van (de wortel van het kwadraat van) de verschillen tussen individuen in de populatie en het gemiddelde, en het aantal metingen in je steekproef.

Bij de Poissonverdeling is de steekproefstandaarddeviatie gelijk aan de wortel uit het getelde aantal:

$s = \sqrt{aantal}$

Stel je telt 50 leukocyten per 0,01 microliter bloed, dan is de standaarddeviatie $s = \sqrt{50} = 7,07$.

Scheve verdelingen

De Poissonverdeling lijkt redelijk symmetrisch, maar is het niet. En aantallen tellen onder de nul zit er ook niet in: -5 vissen per uur kan niet!

Verdelingen kunnen dus ook scheef zijn. Dan is de kansverdeling rondom de piek niet meer symmetrisch, maar een van de staarten is langer.

Bij een links-scheve verdeling (left-skewed) is de linker staart langer. Er zijn dan meer metingen met relatief lage waarden. Het gemiddelde ligt dan links van de piek.

Bij een rechts-scheve verdeling (right-skewed) is de rechter staart langer. Er zijn dan meer metingen met relatief hoge waarden. Het gemiddelde ligt dan rechts van de top,

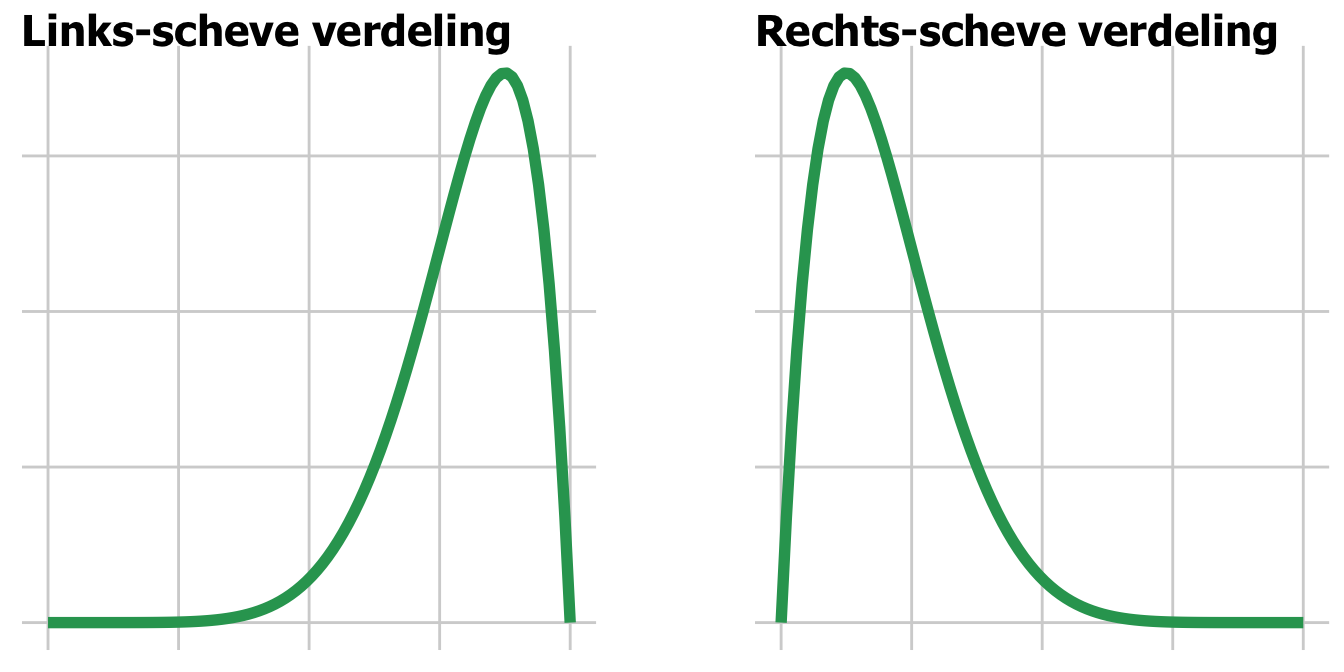
Een scheve verdeling heeft als gevolg dat het gemiddelde geen handige maat meer is voor het midden van je verdeling. Want een lange staart kan het gemiddelde flink opzij trekken!

Bimodale verdeling

Soms vertoont data twee afzonderlijke pieken. Dit wordt een bimodale verdeling genoemd. Een bimodale verdeling zie je als je data hebt die twee verschillende groepen of clusters vertegenwoordigen. Bijvoorbeeld:

de verdeling van lichaamslengte in een dataset met zowel kinderen als volwassenen
het gewicht van twee verschillende soorten fruit, zoals appels en peren

In deze gevallen zie je twee duidelijke pieken in de data, elk corresponderend met een andere groep.

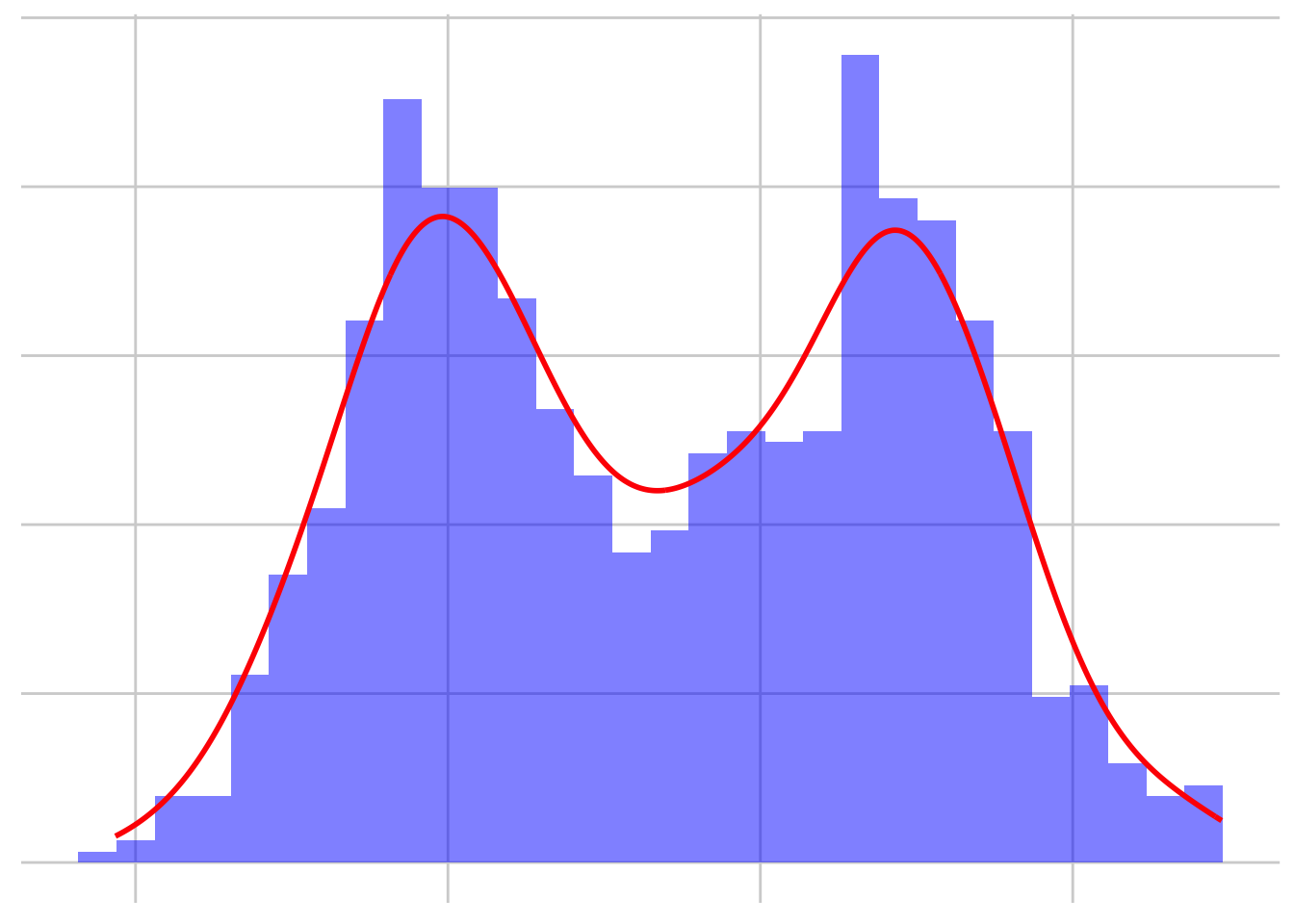
Let op: als je het gemiddelde nu gaat berekenen van alle datapunten in je dataset, komt dat ergens tussen de twee pieken uit. Dat wil je natuurlijk niet, dat zegt niet zoveel. Als je een bimodale verdeling in je data ziet, moet je dus gaan uitvogelen hoe dat komt, en je data in die groepen verdelen.

Is dit nou normaal?

Een normaalverdeling herken je aan de piek in het midden en de symmetrische staarten. Het lijkt een beetje op zo’n oude klok, dus we noemen de normaalverdeling ook wel klokvormig (of bell shaped in het Engels).

Vaak is de vraag “is dit nou normaal verdeeld?”, omdat je met normaal verdeelde data andere dingen kunt dan met niet-normaal verdeelde data. Hoe herken je dan niet-normaal verdeelde data?

Ten eerste: Je kunt dus naar de verdeling kijken. Lijkt hij niet op een normaalverdeling (geen klok-vorm) met de piek in het midden en symmetrische staarten? Dan is het waarschijnlijk niet normaal verdeeld. Ongelijke staarten en de piek niet in het midden zijn duidelijke aanwijzingingen dat de data niet normaal verdeeld is. Vergeet echter niet dat er altijd wat variatie in je data zit, dus bij een steekproef met normaal verdeelde data zal de grafiek ongeveer symmetrisch zijn met ongeveer de piek in het midden.
Ten tweede: als het kwalitatieve data is, dan is het niet normaal verdeeld. Ben je aan het tellen ipv meten? niet normaal verdeeld.
Ten derde: je kan statistisch testen of data normaal verdeeld is. Dat leren jullie in het tweede jaar.

Populatie

$\boldsymbol{\mu}$ en $\boldsymbol{\sigma}$

Veel biologische variabelen zijn dus “normaal verdeeld”, en dat betekent dat we ze kunnen beschrijven met de twee parameters:

(Let op, we hebben het hier dus niet over een steekproef, maar over de hele populatie. Om dat extra duidelijk te maken, kleuren we de hele achtergrond even roze. )

Het populatiegemiddelde ($\mu$), de gemiddelde waarde van de populatie. Deze is gelijk aan de x-waarde, de lengte in dit geval, op het hoogste punt van de grafiek (zie onderstaande figuur). Dit betekent dat als je de lengte van willekeurig persoon meet de kans het grootst is dat die lengte rond de 1,75 meter zal uitvallen.
De populatiestandaarddeviatie ($\sigma$), de variatie / spreiding van de populatie (zie onderstaande figuur). Deze waarde bepaalt de breedte van de curve. Als de normaalverdeling heel smal is, is $\sigma$ heel klein en is in het voorbeeld iedereen ongeveer even lang. Als de normaalverdeling heel breed is, is $\sigma$ heel groot en is er heel veel verschil in lengte.

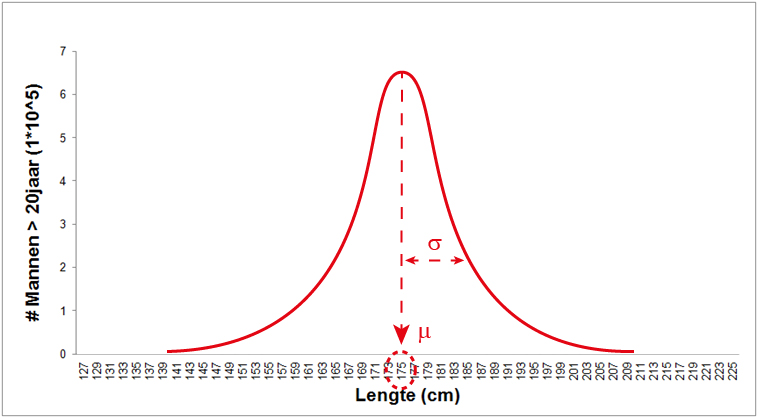
normaalverdeling

Een normaalverdeling is symmetrisch (de linker kant van het midden is het spiegelbeeld van de rechterkant van het midden)
het populatiegemiddelde geeft aan waar het midden ligt (Excel: =AVERAGE() - dan moet je dus wel de complete populatie gemeten hebben)
de populatiestandaarddeviatie geeft aan hoe breed de normaalverdeling is: een maat voor de spreiding. (Excel: =STDEV.P() - dan moet je dus wel de complete populatie gemeten hebben)

Steekproef

$\boldsymbol{\overline{x}}$ en $\boldsymbol{s}$

Het populatiegemiddelde $\mu$ gaf aan waar het midden van de normaalverdeling lag. Meestal is dit populatiegemiddelde iets wat we niet weten, maar wel graag willen schatten. Daarom doen we dan een steekproef.

(We kleuren de hele achtergrond even blauw. )

De data van je steekproef kan ook normaal verdeeld zijn. Sterker nog, als we een steekproef nemen uit een normaal verdeelde populatie, dan wil je graag dat die data ook normaal verdeeld is. Anders heb je namelijk bijkbaar geen random steekproef. Dit soort maten kun je dus ook gebruiken om een steekproef te beschrijven.

Het steekproefgemiddelde ($\overline{x}$), de gemiddelde waarde van de meetpunten.(Excel: =AVERAGE())
De steekproefstandaarddeviatie ($s$), de variatie / spreiding van de meetpunten in je steekproef (Excel: =STDEV.S())

De steekproefstandaarddevaitie bereken je zo (of nou ja, meestal gebruik je Excel, maar dit is de formule):

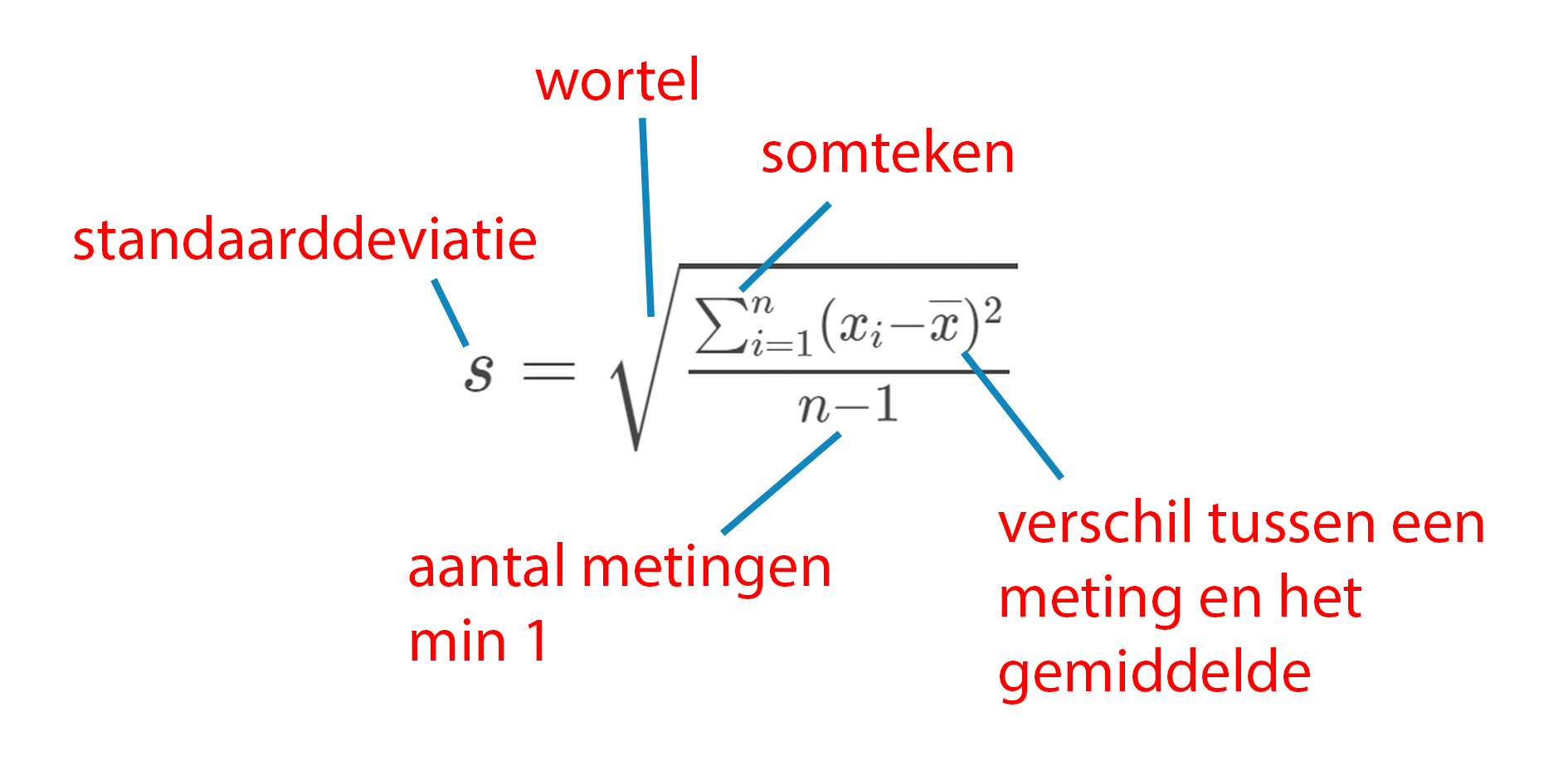
$s$ = steekproefstandaarddeviatie $n$ = aantal metingen $x_i$ = bepaalde meting $\overline{x}$ = steekproefgemiddelde

Oftewel:

Bereken het gemiddelde.
Neem van elk getal de afstand (d) tot het gemiddelde
Neem het kwadraat van die afstanden.
Tel al die kwadraten bij elkaar op.
Deel dat getal door (het aantal metingen - 1)
Neem de wortel van de uitkomst

Kijk, voor dat soort dingen hebben we nou Excel. Excel heeft een functie die de standaard deviatie uit rekent. STDEV.S() voor het uitrekenen van de standaard deviatie van een steekproef (sample) en STDEV.P() voor het uitrekenen van de standaard deviatie van een populatie (population). Kies STDEV.S(), tenzij je echt de hele populatie (!) gemeten hebt. Meestal doe je een steekproef, dus gebruik je STDEV.S().

Typ =STDEV.S( in een cel
Selecteer met de cursor de cellen waarvan de standaard deviatie moet worden uitgerekend.
Sluit af met een haakje en klik op enter

Stel je bijvoorbeeld voor dat we hetzelfde bakje poeder in triplo op 2 weegschalen gemeten hebben:

Het gemiddelde bij beide weegschalen is 30 gram. Maar de spreiding van de metingen is niet gelijk! Kijk maar:

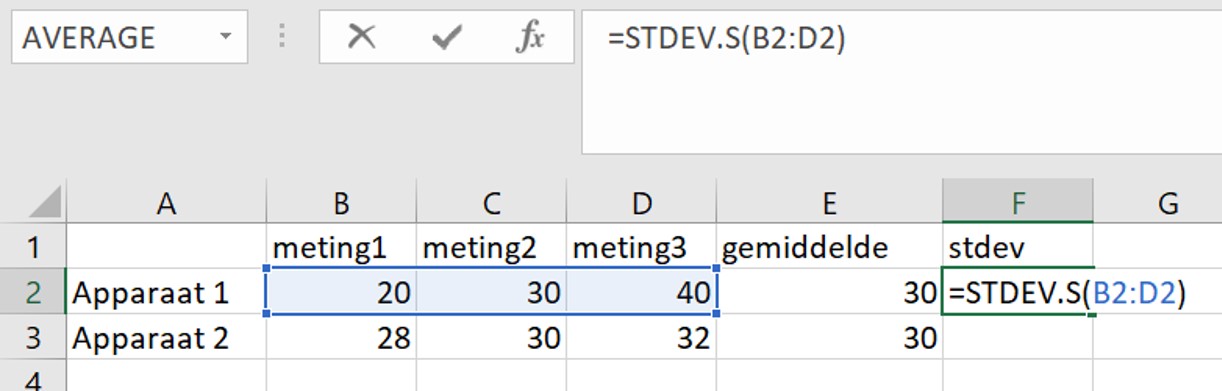
De standaard deviatie is een maat voor de variatie (betrouwbaarheid) van je meetresultaten: Hoe groter de standaard deviatie hoe groter de variatie tussen de metingen (en dus onbetrouwbaarder). Apparaat 1 geeft een grotere variatie van de meetpunten en dus een hogere standaard deviatie in vergelijking met apparaat 2.

Meetwaarden met standaarddeviatie afronden

Bij chemisch rekenen leren jullie over het correct afronden van meetwaarden en rekenregels. Maar als van een meetwaarde een maat van spreiding (meetfout) bekend is, zoals een standaarddeviatie, werkt het net iets anders. Dan bepaalt namelijk de meetfout de precisie waarmee je de meetwaarde op mag schrijven.

Een meetwaarde met meetfout noteer je als meetwaarde ± meetfout.

Dus een steekproefgemiddelde van 5.2 cm met een standaarddeviatie van 0.1 noteer je als: 5.2 ± 0.1 cm.

Voor het afronden van meetwaarden met een meetfout, geldt het volgende:

De meetwaarde en fout schrijven we als dezelfde macht van 10 (of orde van grootte): dus 300 ± 12, of misschien (0,300 ± 0,012) ∙ 10³, maar niet 0,3 ∙ 10³ ± 12 (zie ook het filmpje hierboven over significantie en wetenschappelijke notatie)
We beginnen met het afronden van de meetfout. op 1 significant cijfer
Kijk naar het aantal decimalen die de meetfout nu heeft. Rond je meetwaarde af op hetzelfde aantal decimalen (cijfers na de komma).
zet in wetenschappelijke notatie als het lastig leesbaar is (kan ook als stap 1, dat maakt niet uit)

Dus 0,16635566 ± 0,02333 wordt 0,17 ± 0,02 of (1,7 ± 0,2)∙ 10^-1 (beide zijn goed)

3556 ± 156,3 wordt (3,6 ± 0,2) ∙ 10³.

Wanneer wetenschappelijke notatie?

Bij Chemie&rekenen leren jullie ook over de wetenschappelijke notatie. Maar in het geval van meetfouten en meetwaarden, wanneer moet je hem dan gebruiken?

mag: Als het lastig wordt om te lezen (bijv. 0.000057 ± 0.000002 cm mag je opschrijven als (5.7 ± 0.2)*10^-5. Maar: 0.000057 ± 0.000002 cm is niet fout, wel slecht leesbaar. Beide antwoorden zijn dus goed.)
moet: als je anders meer dan 1 significant cijfer in de meetfout op zou moeten schrijven. (bijvoorbeeld: 381 ± 128 cm afronden –> 128 afronden op 1 significant cijfer is 1 * 10² en niet 100. Want 100 heeft 3 significante cijfers. –> correcte afgeronde antwoord: (4 ± 1) * 10² cm. In dit geval is 400±100 cm of 381 ± 100 cm wel fout!)

95% BI

We doen in deze cursus bijna alleen maar beschrijvende statistiek, we beschrijven onze gevonden data. Inductieve statistiek, om bijvoorbeeld een kans te berekenen bij de vraag of twee populaties van elkaar verschillen, doen we nog niet. Dat gaan we nog doen in jaar 2 van je opleiding.

Toch doen we wel 1 ding op populatie-niveau: ook beschrijven. We hebben al naar verschillende mogelijke verdelingen gekeken (bijv normaalverdeling) om een populatie te beschrijven. Bij een steekproef met een beschrijvende onderzoeksvraag wil je graag weten wat populatiegemiddelde $\mu$ is, maar die kunnen we niet precies achterhalen. Daarom bepalen we steekproefgemiddelde $\overline{x}$ en gaan op basis daarvan een uitspraak (proberen te) doen over $\mu$

Dus stel je wilt de gemiddelde bloedijzerconcentratie van ILC-studenten weten. de meet bloedijzerconcentratie in 30 ILC-studenten (steekproef) en vindt een steekproefgemiddelde van 20 micromol/liter met een steekproefstandaarddeviatie van 5 micromol/liter. Dan zou je op basis daarvan een schatting kunnen geven van de gemiddelde bloedijzerconcentratie van alle ILC-studenten (populatie). Je weet ook, dat als je die steekproef 100 keer zou herhalen, je 100 keer net wat anders zou vinden (zie paragraaf over die kangaroes bovenaan deze les). Dus je schatting kan beter niet zijn “Nou, ik schat precies 20 micromol/liter” , maar liever “Ik schat dat het in de buurt van 20 micromol/liter zit”.

“In de buurt van” is natuurlijk een beetje vaag, dus daar is een oplossing voor gemaakt: die schatting van het populatiegemiddelde $\mu$ doen we met een 95% betrouwbaarheidsinterval (95% BI).

Bijvoorbeeld: op basis van de steekproef hierboven zeg ik (uitspraak) dat het populatiegemiddelde ligt tussen 18 en 22 micromol/liter, en deze uitspraak heeft een betrouwbaarheid van 95%.

Dus:

Wat schat je dat het populatiegemiddelde bloedijzerconcentratie bij ILC-studenten is?
Tussen de 18 en 22 micromol/L
oke, hoe betrouwbaar is die schatting?
95% !

95% is de standaard afspraak over hoe betrouwbaar je uitspraken in dataverwerking moeten zijn. Je kunt natuurlijk ook wel een smalleren schatting geven (bijvoorbeeld tussen 19,98 en 20,02 micromol/L), maar dat weet je een stuk minder zeker. De betrouwbaarheid van die schatting is erg laag. Je kunt ook rustig met een enorme betrouwbaarheid schatten dat de gemiddelde bloedijzerconcentratie bij ILC-studenten tussen de 0 en 300 micromol/L zal zitten. Maar aan die uitspraak hebben we niks, hoe betrouwbaar hij ook is. Vandaar de standaardafspraak van 95%.

Hoe bereken je die grenswaarden?

95% BI Optie 1: >=50 meetpunten

Bij 50 metingen of meer in je steekproef, maak je gebruik van de volgende formule voor het 95% BI:

$\overline{x} \pm 1,96 * \frac{s}{\sqrt{n}}$

$\overline{x}$ : steekproefgemiddelde
$s$: steekproefstandaarddeviatie
$n$ : aantal metingen in de steekproef

steekproefgemiddelde $\overline{x}$ achterhaal je in Excel met =AVERAGE() (of in JASP, zie verderop in les 6).

steekproefstandaarddeviatie $s$ achterhaal je in Excel met =STDEV.S() (of in JASP, zie verderop in les 6). $s$ hangt af van het aantal metingen.

aantal metingen $n$ kun je in Excel tellen met =COUNT(). Of als het er weinig zijn, tel je ze handmatig.

Stel, we vissen 25 katten van straat in Utrecht en meten hun staart, want we willen weten wat de gemiddelde kattenstaartlengte in Utrecht dit jaar is. We vinden een steekproefgemiddelde van 28 cm en een steekproefstandaardeviatie van 3 cm. Dan is het 95% betrouwbaarheidsinterval:

$\overline{x} \pm 1,96 * \frac{s}{\sqrt{n}}$

$1,96 * \frac{3}{\sqrt{25}} = 1,176$ cm

afronden geeft $1$ cm

ondergrens: $28-1 = 27$ cm

bovengrens: $28+1 = 29$ cm

Dus het 95% BI is 27 tot 29 cm

We kunnen met 95% zekerheid zeggen dat de gemiddelde kattenstaartlengte van Utrechtse katten ($\mu$ dus) tussen de 27 en 29 cm ligt. (Vergeet de eenheid niet.)

Leer die manier van uitleggen uit je hoofd. Die 95% gaat over de betrouwbaarheid van jouw schatting. Daarom heet het ook een 95% betrouwbaarheidsinterval (of in het Engels: 95% confidence interval: zekerheidsinterval). Hij gaat dus niet over de kans dat het ware populatiegemiddelde tussen die onder- en bovengrens ligt.

goed: Je kan met 95% zekerheid zeggen dat het populatiegemiddelde ligt tussen …. en …
fout: Er is een kans van 95% dat het populatiegemiddelde ligt tussen …. en …
fout: 95% van de datapunten ligt tussen … en …
fout: 95% van de populatie ligt tussen … en …

Een 95% BI berekenen we alleen als we het populatiegemiddelde niet weten. Als we populatiegemiddelde $\mu$ weten, hoeven we hem ook niet met 95% betrouwbaarheid te gaan lopen schatten. Tenzij we een $\mu$ weten, maar we willen controleren of die wel klopt, met een steekproef.

95% BI Optie 2: <50 meetpunten

Onder de 50 metingen hangt je schatting nog wat meer af van hoeveel metingen je nou precies had. In plaats van 1,96 (die kwam uit een normaalverdeling), gaan we de schatting van het populatiegemiddelde (want daar waren we mee bezig, remember?) nu een beetje breder maken. Hoeveel breder, hangt af van hoeveel metingen je hebt. We schrijven dus een $t$ (uit de t-verdeling, een zusje van de normaalverdeling) in de formule in plaats van de 1,96 (en die $t$ is altijd groter dan 1,96):

$\overline{x} \pm t * \frac{s}{\sqrt{n}}$

$\overline{x}$ : steekproefgemiddelde
$t$ : t-waarde
$s$: steekproefstandaarddeviatie
$n$ : aantal metingen in de steekproef

De $t-waarde$ moeten we in een tabel opzoeken. Die tabel staat op het formuleblad. In de t-tabel staat steeds de $t-waarde$ voor een aantal vrijheidsgraden. Dat is het aantal meetpunten min 1:

$vrijheidsgraden = n-1$

Dat heeft er mee te maken, dat je bij n metingen, soort van n-1 keuzes hebt. Stel je bijvoorbeeld voor dat je 6 verschillende kleuren Skittles hebt. Je kan 5 keer kiezen welke kleur Skittle je als volgende op gaat eten, maar de 6e keer heb je niks meer te kiezen, er is er nog maar 1 over.

Stel, we vissen 16 katten (n=16) van straat in Groningen en meten hun staart, want we willen weten wat de gemiddelde kattenstaartlengte in Groningen dit jaar is. We vinden een steekproefgemiddelde $\overline{x}$ van 26 cm. en een steekproefstandaarddeviatie $s$ van 5 cm. Dan is het 95% betrouwbaarheidsinterval:

$\overline{x} \pm t * \frac{s}{\sqrt{n}}$

dus we moeten uitrekenen: $t * \frac{5}{\sqrt{16}}$ cm

$t$ zoeken we op in de tabel bij vrijheidsgraden $n-1 = 16-1 = 15$. Dat geeft $t = 2,131$

$2,131 * \frac{5}{\sqrt{16}} = 2.66375$ cm

afronden op 1 significant cijfer geeft $3$ cm

ondergrens: $26-3 = 23$ cm

bovengrens: $26+3 = 29$ cm

Dus het 95% BI is 23 tot 29 cm : onze schatting is dat Groningse katten een gemiddelde staartlengte hebben van tussen de 23 en 29 centimeter.

Extra oefenen deel 1: gemiddelde ± standaarddeviatie afronden

Opdracht 4

Rond de volgende meetwaarden met meetfout af volgens de regels:

8,675 ± 1,456
776578 ± 1875
77,87767 ± 0,0356
3445 ± 15
0,0000022333 ± 0,02
0,0023454 ± 0,000244
0,0023454 ± 0,000164
165,45639 ± 0,011467
165,4563946 ± 0,00011467
165,4563946 ± 0,00011567
165,45639 ± 0,11467
165,45639 ± 0,21467
165,45439 ± 0,025
165,45639 ± 0,0250001
165,45669 ± 0,0035
23,5 ± 1
32,5 ± 12
666 ± 19
666 ± 129
5,3 ± 1,65

Klik hier voor de antwoorden

jaar	gemiddelde
8,675 ± 1,456	9 ± 1
776578 ± 1875	(777 ± 2) *10³
77,87767 ± 0,0356	77,88 ± 0,04
3445 ± 15	(345 ± 2) *10¹
0,0000022333 ± 0,02	0,00 ± 0,02
0,0023454 ± 0,000244	(2,3 ± 0,2) * 10^-3
0,0023454 ± 0,000164	(2,3 ± 0,2) * 10^-3
165,45639 ± 0,011467	165,46 ± 0,01
165,4563946 ± 0,00011467	165,4564 ± 0,0001
165,4563946 ± 0,00011567	165,4564 ± 0,0001
165,45639 ± 0,11467	165,5 ± 0,1
165,45639 ± 0,21467	165,5 ± 0,2
165,45439 ± 0,025	165,45 ± 0,03
165,45639 ± 0,0250001	165,46 ± 0,03
165,45669 ± 0,0035	165,457 ± 0,004
23,5 ± 1	24 ± 1
32,5 ± 12	( 3 ± 1) *10¹
666 ± 19	( 67 ± 2) *10¹
666 ± 129	( 7 ± 1) *10²
5,3 ± 1,65	5 ± 2

Extra oefenen deel 2: de invloed van de standaarddeviatie op normaalverdeling

Voor dit onderdeel heb je het bestand Normaalverdeling.xlsx nodig. Download hier (klik) de data

Open dit bestand en klik met de rechtermuisknop op de naam van de worksheet “normaal_verdeling” links onder op de pagina.
In het venster dat opent, klik op Move or Copy.
Selecteer move to end en vink aan Create a copy. Klik OK.

De kopie staat nu als extra werkblad naast het originele werkblad.

Het creëren van een kopie dient als back-up. Bewaar altijd je ruwe data in een apart werkblad (of een apart bestand), maak een kopie en ga de kopie bewerken in Excel.

In het tabblad “normaal_verdeling” is de standaard normaalcurve weergeven volgens de formule (die je niet uit je hoofd hoeft te leren):

$f(x)=\frac{1}{σ\sqrt{2π}}e^{-\frac{1}{2}}(\frac{x-\mu}{\sigma})^2$

Als je op cel B5 klikt, kun je bovenin de formulebalk zien dat we die niet uitgetypt hebben in excel. Excel heeft er al een formule voor: NORM.DIST(). In cel B5 staat =NORM.DIST(A5;$B$1;$B$2;FALSE), wat zoveel betekent als:

gebruik de normaalverdeling om een Y-waarde te maken met:
de X-waarde in cel A5
het gemiddelde (mu) in cel B1, en als ik deze formule kopieer moet hij altijd precies naar B1 verwijzen (dat zijn de $ tekentjes).
de standaarddeviatie (sigma) in cel B2, en als ik deze formule kopieer moet hij altijd precies naar B2 verwijzen (de $ tekentjes).
maak hem niet cummulatief (deze functie kan twee soorten grafieken maken, we willen de gewone)

Je kan op fx klikken naast de formulebalk voor meer info over een formule:

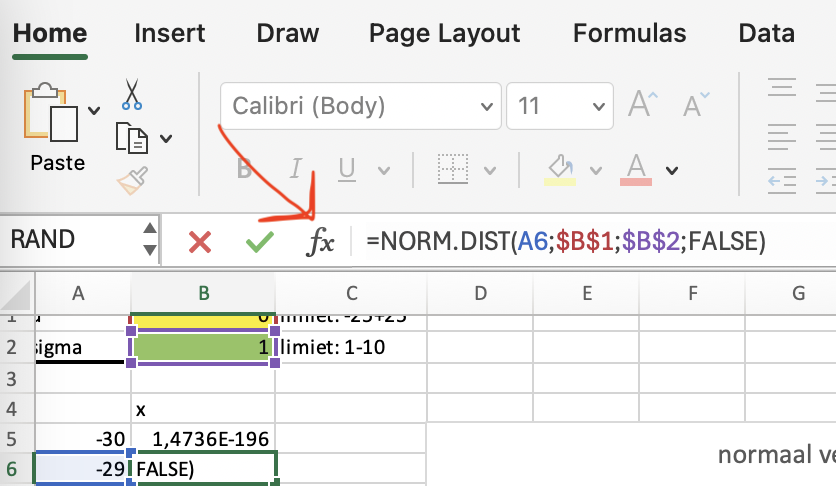
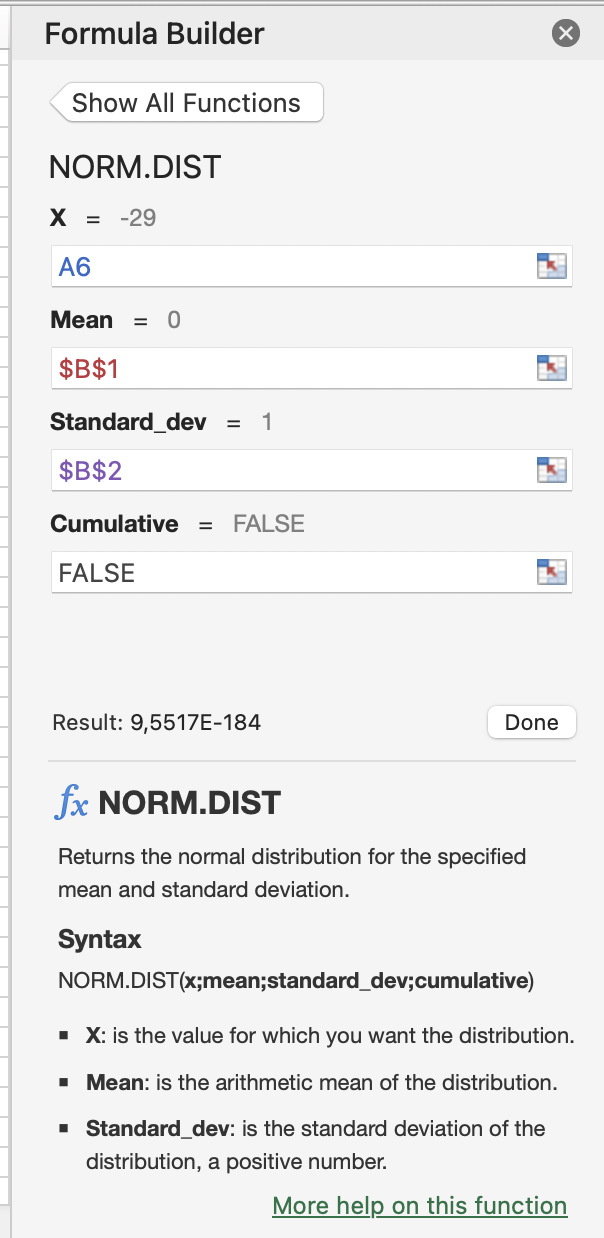
De standaard functie heeft een $μ$ (mu) van 0 (gele vak B1) en een $σ$ (sigma) van 1 (groene vak B2). In die vakken kun je de parameters voor deze normaalverdeling instellen. Deze nummertjes kun je dus veranderen om te kijken wat er gebeurt. (doet cel B5 het per ongeluk niet meer, kopieer hem dan even van je andere tabblad met je backup.)

De getallen in kolom B veranderen. Dit zijn de Y-waardes die de normaalverdeling heeft bij X-waarden -30 tot en met +30, bij de $μ$ en $σ$ die je net ingesteld hebt.

Exercise 4

Wat gebeurt er met de grafiek als de spreiding ($σ$) toeneemt?

Klik hier voor het antwoord

De grafiek wordt breder en lager (minder hoog).

Exercise 4

Wat gebeurt er met de grafiek als de spreiding ($μ$) afneemt?

Klik hier voor het antwoord

De grafiek verandert niet van vorm, maar verschuift naar links op de x-as.

Exercise 4

We gaan naast elkaar kolommen maken met datapunten die een normaalverdeling volgen met 5 verschillende standaarddeviaties.

Vul bij $μ$ een 0 in (nul)
Vul bij $σ$ een 1 in
selecteer alle Y-waarden in kolom B, dat zijn cellen B5 t/m B65 (klik op B5, druk shift in, klik op B65)
kopieer ze (ctrl-C)
klik op vak M5 en kies bovenin je taakbalk paste special > paste values
De cellen M5:M65 worden nu gevuld met nummers

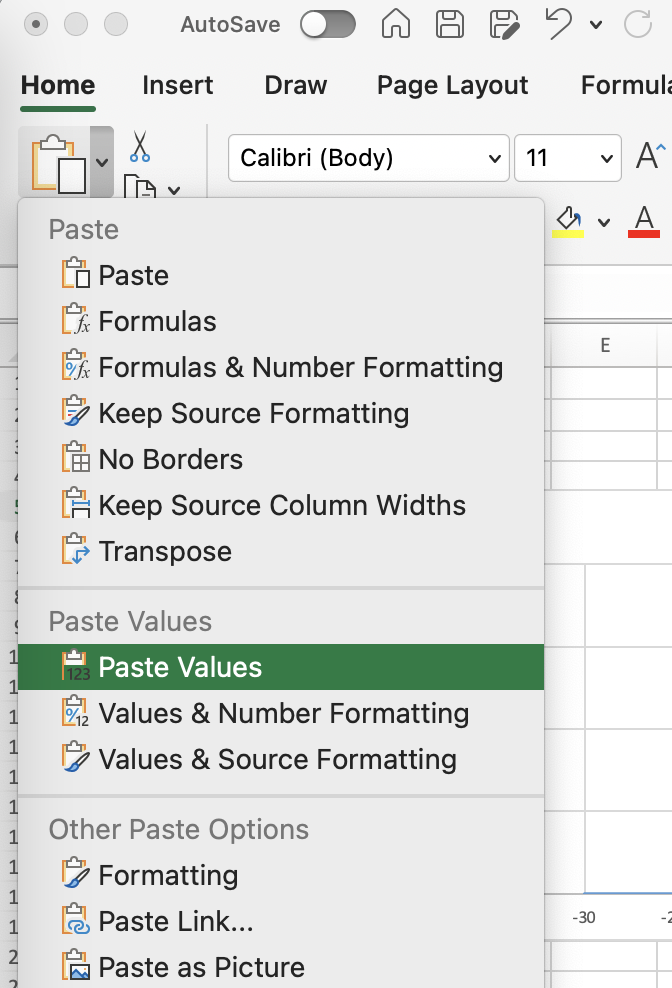
Laat bij $μ$ een 0 staan
Vul bij $σ$ nu een 2 in
kopieer en plak op dezelfde manier als net met paste special > paste values de Y-waarden naar de cellen N5:N65
Herhaal dit ook voor $σ$ met de waardes 3, 4 en 5. Voor iedere $σ$, kopieer B5:B65 met paste special > paste values naar respectievelijk:
```
`M5:M65`     σ=1
`N5:N65`     σ=2
`O5:O65`     σ=3
`P5:P65`     σ=4
`Q5:Q65`     σ=5
```
Maak een grafiek type scatter plot with smooth lines voor de verschillende normaalcurves.

Klik hier om te controleren hoe het er uit zou moeten zien

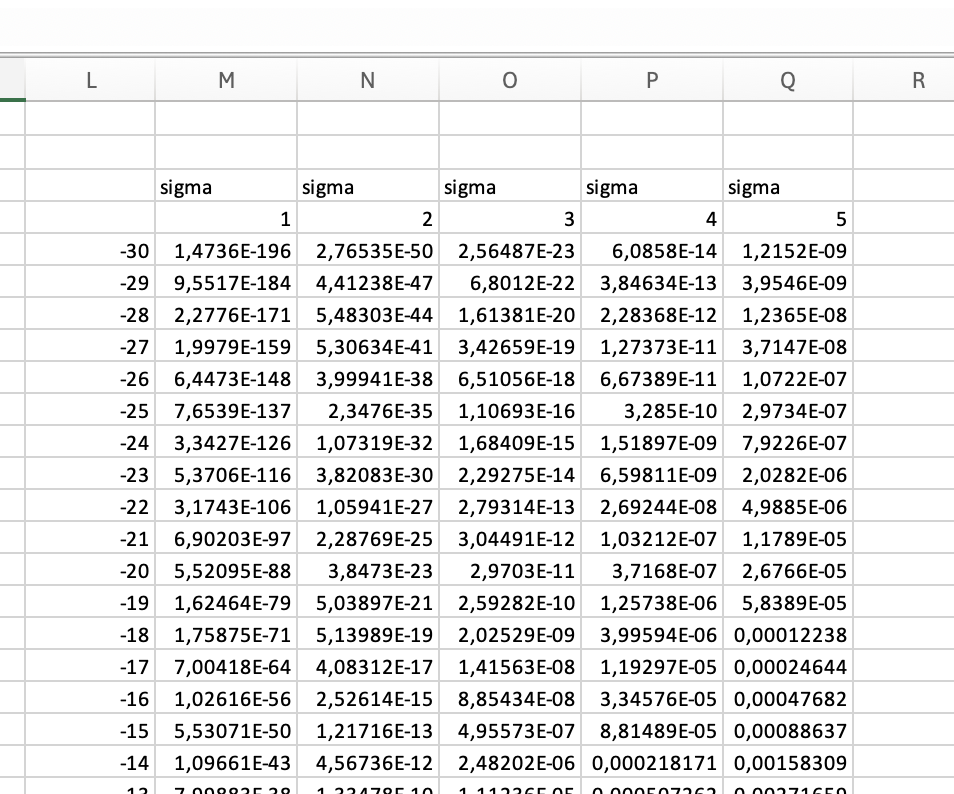
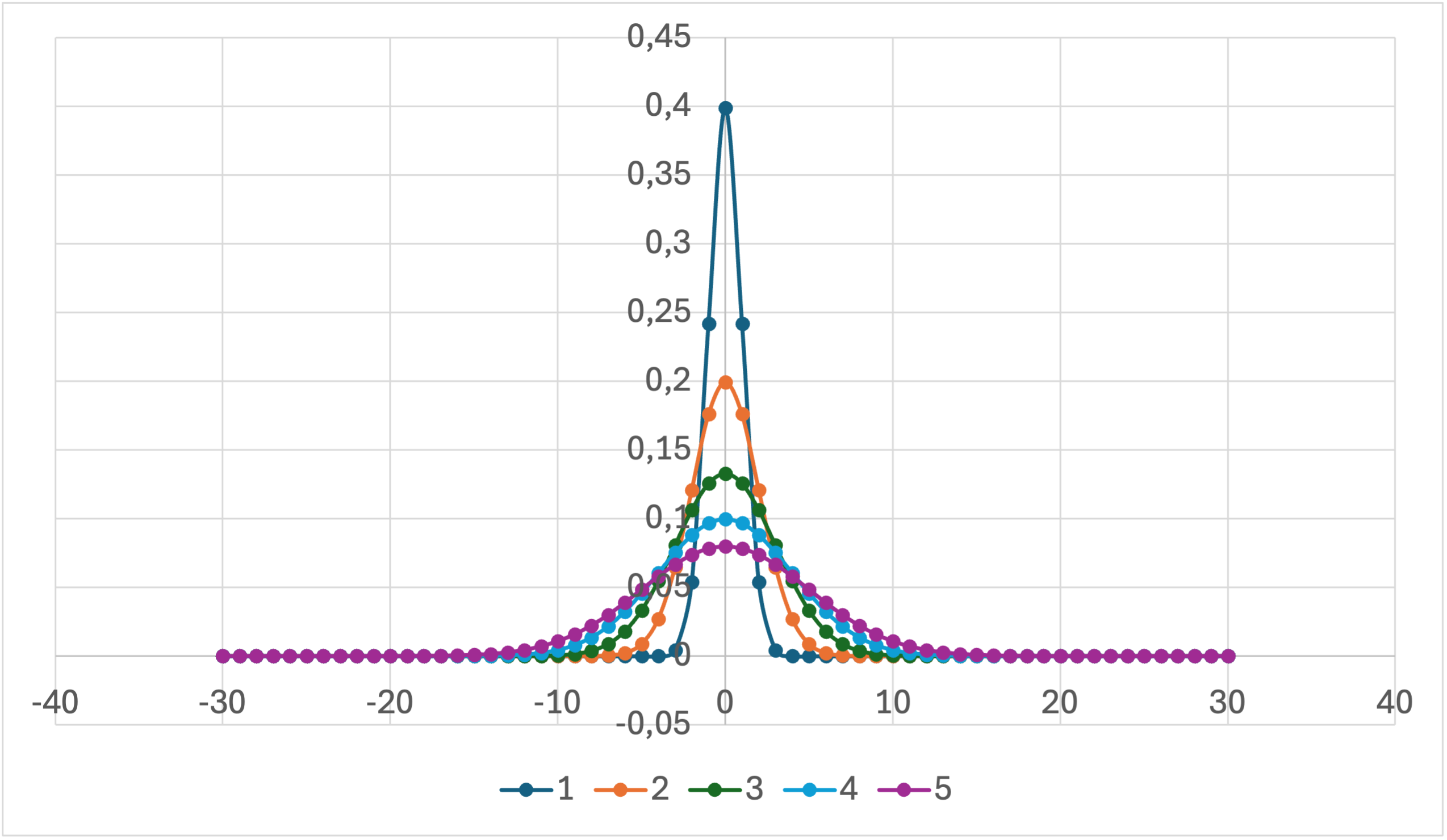
Zoals je kan zien vertelt de breedte van een normaalverdeling je iets over de variatie in deze populatie. Hoe breder, hoe variabeler.

Steekproefdata uit een normaal verdeelde populatie, geven we vaak weer met een staafdiagram. Je hebt er een gemaakt in les 2, waar ook duidelijk werd dat je zonder maat voor de variatie in je data, eigenlijk nog niet zoveel kan aflezen aan een (staaf)grafiek. Die maat gaan we nu toevoegen.

Extra oefenen deel 3: steekproefgemiddelde en steekproefstandaarddeviatie.

Opdracht 4

Ga verder in staartvergelijking.xlsx van les 2 voor het bestand met kattenstaartlengtes in cm van katten in de Lindelaan en aan de Hoofdweg. In beide straten deden we een steekproef.

Bereken voor de katten aan de Lindelaan en voor die aan de Hoofdweg de standaarddeviatie van staartlengte.

Klik hier voor het antwoord

2.90 cm voor de Lindelaan en 4.63 cm voor de Hoofdweg.

Die standaarddeviaties zouden best informatief zijn in ons staafgrafiekje. Laten we hem toevoegen.

Klik op je grafiekje van vorige opdracht, en voeg als volgt foutenbalken toe (let op, klik NIET op standard deviation!! Oh Excel…)

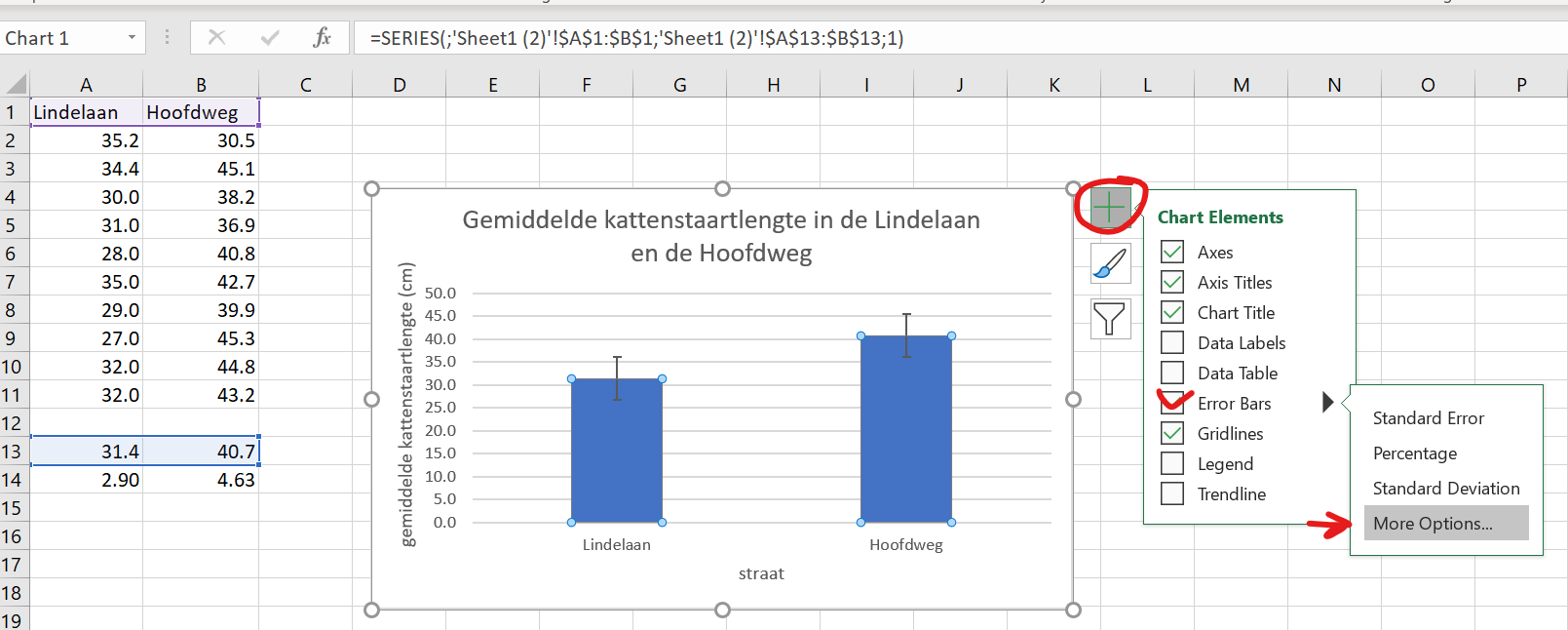
Selecteer voor de errorbars beide standaarddeviaties. Voor zowel de Positive Error Value als de Negative Error Value.

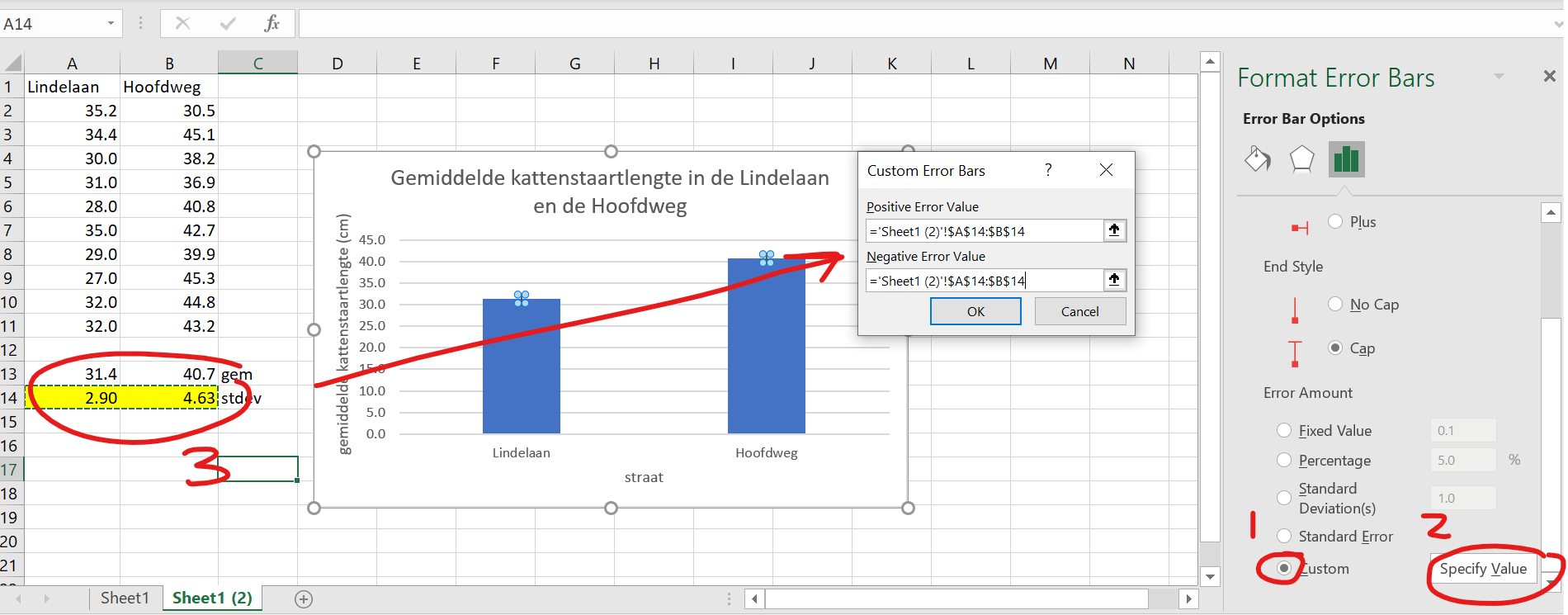
En voila, je hebt spreiding aangegeven in je staafdiagram!

Werkcollege

Professor Kemhoewatoelak is geintereseerd in de gemiddelde lengte van Nederlandse mannen, hij krijgt van het Centraal Bureau van Statistiek de gemeten lichaamslengtes vanuit een steekproef van 100 Nederlandse mannen (zie onderstaande tabel). Op basis van die steekproef wil hij met 95% betrouwbaarheid aangeven hoe lang de gemiddelde Nederlandse man is.

Visualiseer de data aan de hand van een histogram
Controleer de data en verwijder eventuele outliers als dat verantwoord is en beargumenteer waarom je deze weg laat
Bereken het 95% betrouwbaarheidsinterval en noteer de onder- en bovengrens van het 95% BI
Geef ook het 95% BI weer in het histrogram met behulp van twee stippellijnen (onder- en bovengrens)

Table 9: CBS data steekproef lichaamslenge van 100 Nederlandse mannen
A	B	C	D	E
1.94	1.89	1.93	2.04	2.00
1.98	1.98	1.98	1.95	2.04
2.16	1.91	1.87	1.97	1.96
2.01	1.93	2.21	1.91	12.06
2.01	1.94	2.12	1.89	1.98
2.17	1.83	1.89	2.03	2.03
2.05	2.08	1.96	2.04	2.11
1.87	2.02	1.95	2.01	2.04
1.93	1.89	2.08	2.09	1.97
1.96	2.13	1.99	2.21	2.11
2.12	2.04	2.03	1.95	2.10
2.04	1.97	2.01	1.81	2.05
2.04	2.09	2.02	2.11	2.02
2.01	2.09	2.14	1.93	1.94
1.94	2.08	1.98	1.93	2.14
2.18	2.07	2.15	2.11	1.94
2.05	2.06	1.85	1.97	2.20
1.81	1.99	2.06	1.88	2.15
2.07	1.97	2.01	2.02	1.98
1.95	1.96	2.02	1.99	1.90