6: Grafieken lezen en beoordelen
Leerdoelen
De vaardigheden die je zal verwerven tijdens deze les:
- Je leert de voorwaarde waaraan een (wetenschappelijk) figuur moet voldoen
- Vanuit een bestaande figuur het experimenteel ontwerp bepalen
- Lezen en interpreteren van staafdiagrammen, spreidingsdiagrammen en lijngrafieken
- Lezen en interpreteren van Michaelis-Menten grafiek
- Je leert de kenmerken van een slecht figuur te herkennen
- Je leert hoe een slecht figuur omgezet kan worden naar een goed figuur die voldoet aan de wetenschappelijke criteria
Introductie
Om een onderzoeksvraag te beantwoorden worden er experimenten uitgevoerd. De resultaten van een experiment worden samengevat in een figuur, zodat in één oogopslag (althans dat is de bedoeling) duidelijk is wat de uitkomst is van een experiment. Een goed figuur bevat alle relevante informatie en moet “zichzelf” kunnen lezen. Het goed leren lezen en intepreteren van een figuur is daarom een essentieel onderdeel van het werk van een onderzoeker. Het maken van een goede figuur lijkt vanzelfsprekend, maar er zijn veel voorbeelden van slechte figuren en zelf misleidende figuren.
In werkcollege 2 hebben jullie geleerd hoe je een grafiek moet maken en waaraan een goede grafiek moet voledoen. In deze les gaan we aan de slag met het lezen en interpreteren van bestaande grafieken.
Er ziin verschillende soorten grafieken, die gebruikt worden in de Life Science. De meestvoorkomende grafieken zijn:
- Staafdiagram
- Spreidingsdiagram
- Lijngrafiek
- Boxplot
- Histogram
Voordat we specifiek ingaan hoe de verschillende figuren gelezen / geïnterpreteerd moeten worden eerst wat algemene handvatten.
Voorbereiding
Lees ter voorbereiding van deze les Deel 1 in het werkcollege door (zie hieronder). De opdrachten gaan jullie in de les maken.
Werkcollege
Deel 1: Grafieken lezen en interpreteren
Lezen van een grafiek
De eerste stap is om de figuur te beschrijven:
- Wat is het modelsysteem (Aan wie of wat is er gemeten) -> bijvoorbeeld mensen , proefdieren, cellen, eiwitten enz.
- Hoe vaak is er gemeten: biologische vs technische replica’s.
- Wat staat er op de x-as en de y-as (wat is er gemeten)
- Eenheid: wat is de eenheid van de schalen
- Schaal: wat is de schaal van de assen (lineair of logaritmisch)
- Legenda: wat wordt er vergeleken in de grafiek. In het bijschrift staat vaak een deel van deze informatie, en daarnaast vaak andere belangrijke details.
Interpreteren van een grafiek
- Nadat we de grafiek hebben beschreven kunnen we gaan bepalen welk patroon / trend we zien
- Wat is de variatie van de meetpunten?
- Is er veel spreiding tussen de meetgegevens of is de data juist betrouwbaar?
- Zijn er uitbijters aanwezig?
- Wat is de conclusie van de grafiek?
Staafdiagram
Een staafdiagram wordt gebruikt om categorieën of groepen met elkaar te vergelijken (verschilvragen). In Life Science zijn de verschillende groepen de zogenaamde “experimentele” groepen. In de groepen zitten items waaraan gemeten wordt. Deze items kunnen mensen, proefdieren, cellen, eiwitten enzovoorts zijn. Eén groep is de referentie groep. Dit is meestal de controle groep die geen behandeling heeft gekregen. De andere groep(en) hebben wel een behandeling gekregen. De verschillende experimentele groepen staan op de x-as. Vervolgens wordt iedere groep gemeten. Wat er gemeten wordt (de variabele) hangt af van de onderzoeksvraag. De waarden van iedere groep worden samengevat door het gemiddelde of mediaan te berekenen en is evenredig met de lengte van de staaf. In sommige gevallen wordt er “geteld” hoe vaak iets voorkomt in iedere experimentele groep. De meetwaarde van iedere groep is af te lezen op de y-as
Een wetenschappelijk experiment kan samengevat worden met het onderstaande schema:
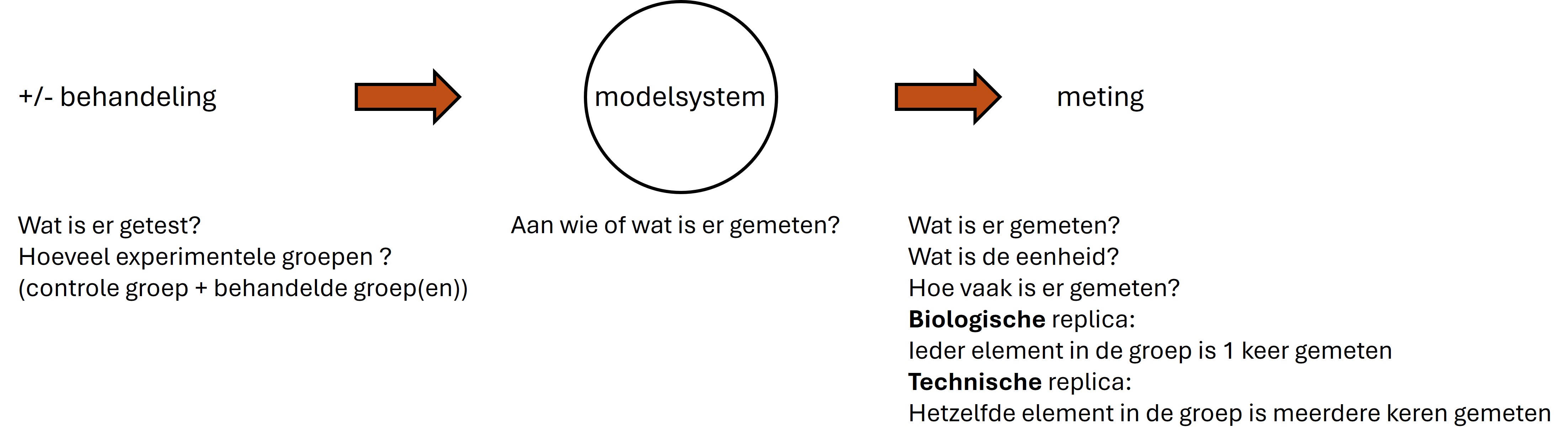
BELANGRIJK:
De meetwaarden kunnen ook relatief uitgedrukt worden ten opzichte van een referentie groep (meestal de controle groep):
- toename / afname uitgedrukt als percentage Hierbij is de waarde van de referentie groep dus altijd 100 %
- toename / afname uitgedrukt als “fold inductie”. Hierbij worden alle meetwaarden per groep gedeeld door de meetwaarde van de controle groep. Bij “fold inductie” is de waarde van de referentie groep dus altijd 1
Voor de interpretatie van een staafdiagram worden de verschillende experimentele groepen met elkaar vergeleken:
- Is er een verschil tussen de referentie groep (controle) en de andere experimentele groepen?
- Hoe groot is dit verschil?
- Is het biologische relevant?
- Hoe groot is dit verschil?
- Werkt de behandeling wel of niet?
Opdracht 6
- Beschrijf de onderstaande grafiek aan de hand van de hierboven genoemde 6 criteria
- Wat is de variatie van de meetpunten?
- Interpreteer de grafiek. Wat is je conclusie?
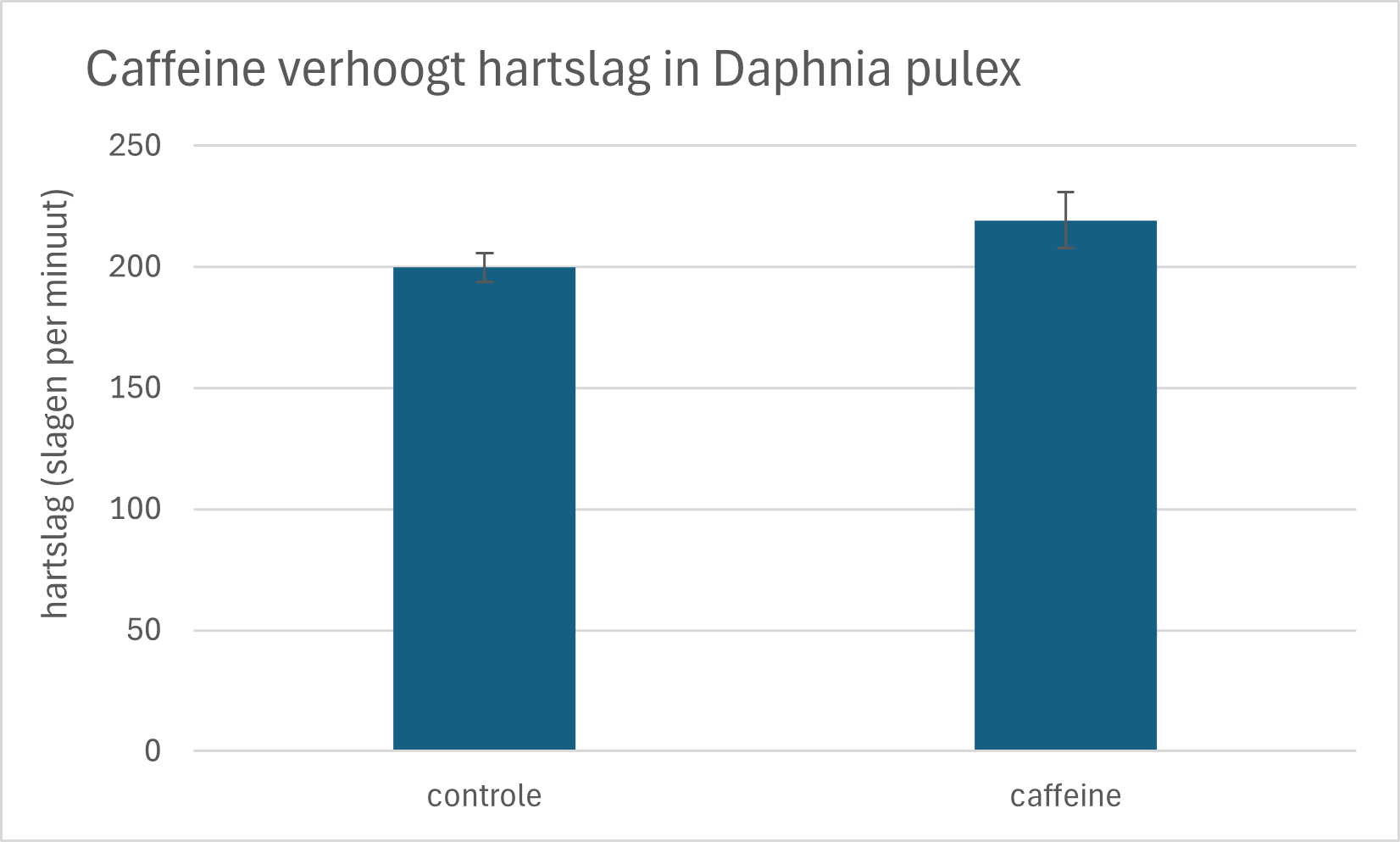
Figure 50: Watervlooien (Daphnia pulex, n=30) zijn blootgesteld aan caffeïne (1 mg/L) voor een tijdsduur van 1 uur. De controle groep (n=30) is niet blootgesteld aan caffeIne. Watervlooien werden geplaatst onder een microscoop en de hartslag werd gemeten door de het aantal hartslagen te tellen voor een periode van 1 minuut. Foutbalken geven de standaard deviatie weer
Opdracht 6
Een student herhaalt het experiment van figuur 1. De data is weergegeven in figuur 2
Interpreteer de grafiek. Wat is je conclusie?
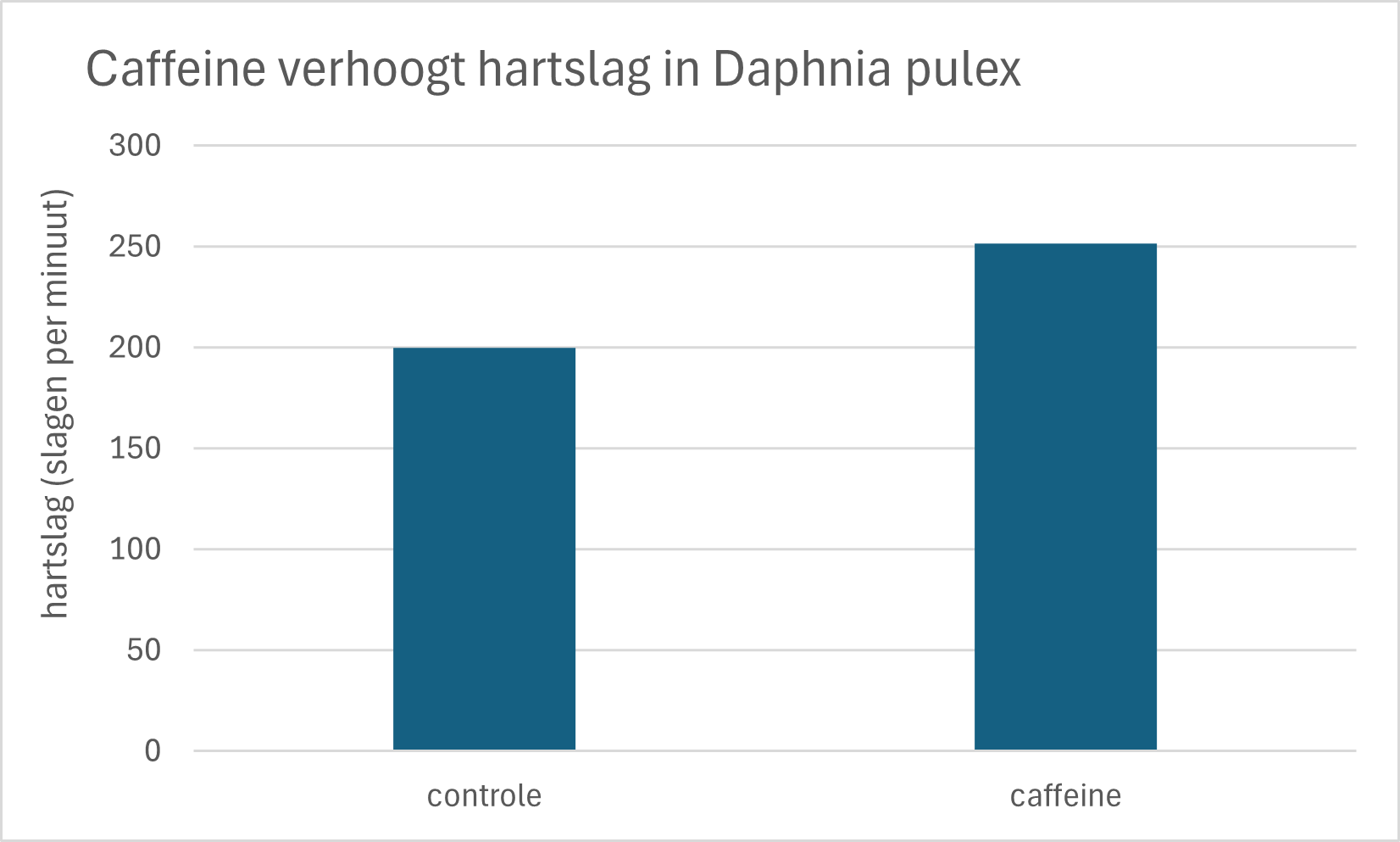
Figure 51: Watervlooien (Daphnia pulex, n=30) zijn blootgesteld aan caffeïne (1 mg/L) voor een tijdsduur van 1 uur. De controle groep (n=30) is niet blootgesteld aan caffeïne. Watervlooien werden geplaatst onder een microscoop en de hartslag werd gemeten door de het aantal hartslagen te tellen voor een periode van 1 minuut.
Opdracht 6
- Beschrijf de onderstaande grafiek aan de hand van de hierboven genoemde 6 criteria
- Wat is de variatie van de meetpunten?
- Interpreteer de grafiek. Wat is je conclusie?
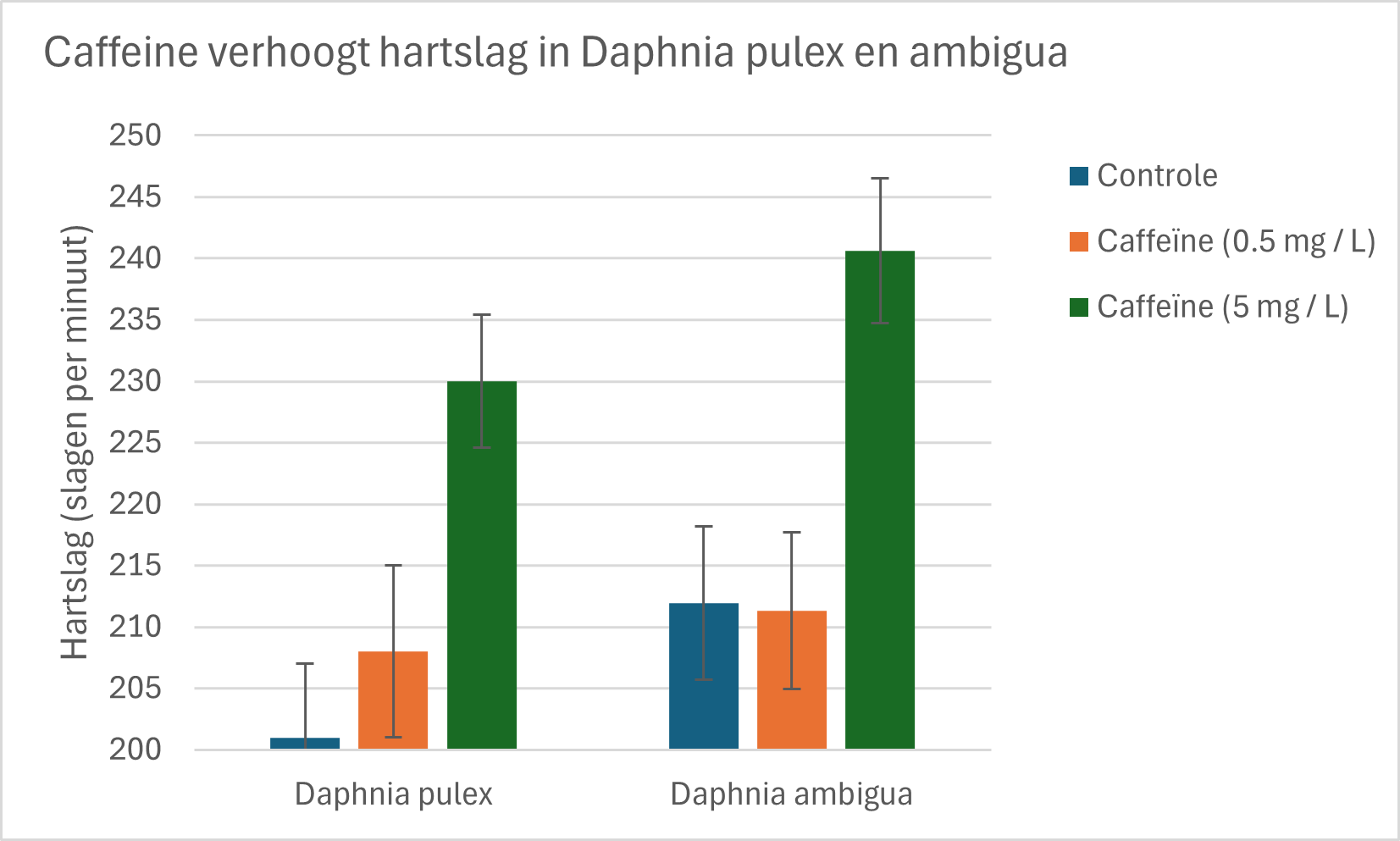
Figure 52: Watervlooien Daphnia pulex en Daphnia ambigua (n=25) zijn blootgesteld aan caffeine (0.5 en 5 mg/L) voor een tijdsduur van 30 minuten. De controle groepen (n=25) zijn niet blootgesteld aan caffeine. Watervlooien werden geplaatst onder een microscoop en de hartslag werd gemeten door de het aantal hartslagen te tellen voor een periode van 1 minuut. Foutbalken geven de standaard deviatie weer
Opdracht 6
Open de volgende link
https://bmccomplementmedtherapies.biomedcentral.com/articles/10.1186/s12906-023-04261-9
- Beschrijf figuur2 aan de hand van de hierboven genoemde 6 criteria. (“Vehicle” betekent hier het oplosmiddel zonder CAEO)
- Wat is de variatie van de meetpunten?
- Interpreteer de grafieken. Wat is je conclusie?
- Werp nog een kritische blik op deze figuur. Zijn alle balken nodig?
Spreidingsdiagram
Een spreidingsdiagram (ook wel scatterplot genoemd) is een grafiek die wordt gebruikt om de correlatie (verbandvragen) tussen twee variabelen te visualiseren. Stel je voor dat je een onderzoek doet naar de relatie tussen studietijd en cijfers. Je hebt een groep studenten gevraagd hoeveel uren ze hebben gestudeerd (de eerste variabele) en welk cijfer ze hebben gehaald (de tweede variabele). Een spreidingsdiagram heeft twee assen. De horizontale as (x-as) staat voor de ene variabele, bijvoorbeeld het aantal uren gestudeerd. De verticale as (y-as) staat voor de andere variabele, bijvoorbeeld het behaalde cijfer. Elk punt in het diagram vertegenwoordigt één student. Door naar het geheel van de punten te kijken, kun je zien of er een patroon is. Als de punten bijvoorbeeld een stijgende lijn vormen, kan dat betekenen dat meer studietijd leidt tot hogere cijfers (positieve correlatie). Als de punten meer willekeurig verspreid zijn, is er mogelijk geen duidelijk verband.
Voor de interpretatie van een spreidingsdiagram wordt er gekeken of er een correlatie / verband is tussen de twee variabelen. De richting van een puntenwolk kan samengevat worden in een trendlijn waarvan de richting de correlatie tussen de variabelen weergeeft.
- positieve correlatie: met een toename van de x-as variabele gaat de andere variabele omhoog (oplopende lijn)
- negatieve correlatie: met een toename van de x-as variabele gaat de andere variabele omlaag (aflopende lijn)
- geen correlatie: met een toename van de ene variabele blijft de andere variabele gelijk (rechte lijn)
Als er een verband is tussen twee variabelen, hoe ziet dit verband er dan uit?
- lineair
- niet-lineair
- exponentieel
- logaritmisch
- hyperbool
LET OP: Als er een verband is waar te nemen in een spreidingdiagram betekent dat niet dat er een oorzaak en gevolg is (causaal verband). Willekeurige variabelen kunnen ook een verband laten zien. Dit wordt spurious correlation genoemd en (leuke) voorbeelden zijn te vinden op deze website
Een toepassing waarbij de spreidingsgrafiek wordt gebruikt is de kalibratielijn. Hierbij wordt een concentratiereeks van een bepaalde stof gemeten op een bepaald apparaat (meestal een photospectrometer). De concentratie reeks staat op de x-as en de waarde van de meting op de y-as. Met behulp van de kalibratielijn kan vervolgens worden teruggerekend hoeveel van de bepaalde stof aanwezig is in een onbekend monster. De kalibratielijn moet een lineair verband laten zien (rechte lijn). Alle concentraties die buiten de rechte lijn vallen, zijn niet bruikbaar.
Opdracht 6
- Beschrijf de onderstaande grafiek aan de hand van de 6 criteria (van les 1). Kijk goed naar het bijschrift om te weten wat de onderzoekers hebben gedaan.
- Wat is de variatie van de meetpunten? Zou je met deze data een grotere of kleinere spreiding in meetwaarden verwachten dan bij een kalibratiecurve?
- Interpreteer de grafiek. Wat is je conclusie?
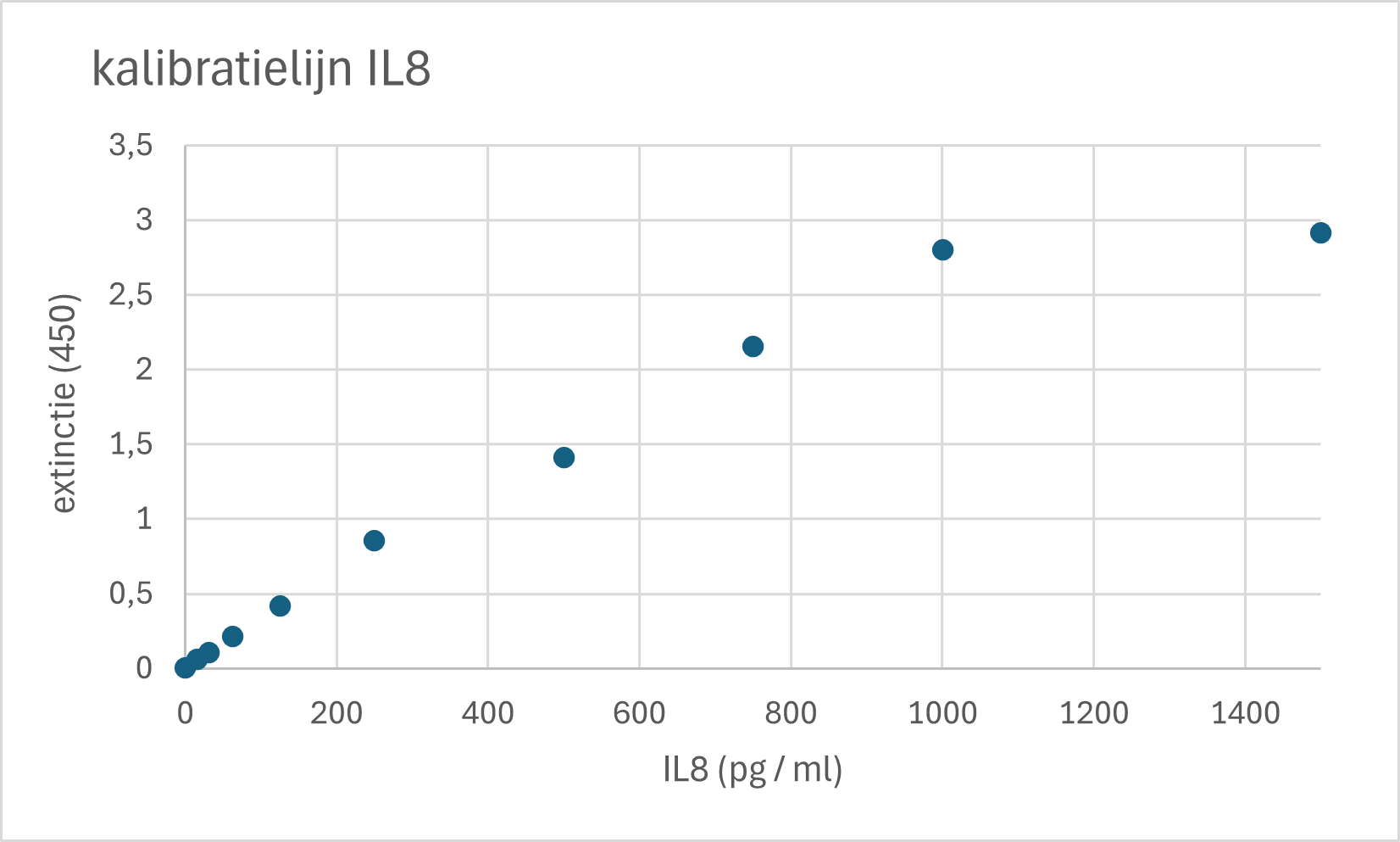
Figure 53: Verschillende concentratie van IL-8 zijn gemeten op een photospectrometer (450 nm) . Elk datapunt is het gemiddelde van twee metingen
Opdracht 6
- Beschrijf de onderstaande grafiek aan de hand van de 6 criteria (van les 1) Deze figuur is afkomstig uit het volgend artikel
- Wat is de variatie van de meetpunten?
- Interpreteer de grafiek. Wat is je conclusie?
](images/05_dave_les2_grafiek_5.png)
Figure 54: The scatter plot of cortisol concentration (QCA versus routine method). A total of 330 human bloodsamples were measured by two different methods. The X-axis represents the value of cortisol concentration measured by the routine method. The Y-axis represents the value of cortisol concentration measured by the QCA method. Te red line represents the regression line. This figure is adapted from this article
Lijngrafiek
Een lijngrafiek is een grafiek die datapunten met een lijn verbindt om een (lokale) trend te visualiseren (vaak voor beschrijvende vragen). De variabele op de x-as is continu en numeriek (dus geen categorieën) , bij voorkeur met vergelijkbare intervallen. De x-as omvat meestal tijdreeksen, concentraties of een andere toenemende eenheid. De grootte van de intervallen op de x-as wordt door de onderzoeker van te voren zelf bepaald.
Voorbeelden van data waarvoor lijngrafieken geschikt zijn:
- tumorgrootte per week na behandeling.
- Aantal nieuwe kinkhoest besmettingen in Nederland.
- gemeten enzymactiviteit bij toenemende substraatconcentraties
Voor de interpretatie van een lijngrafiek wordt er gekeken welke (lokale) /trend er zichtbaar is.
- positieve trend: met een toename van de x-as variabele gaat de andere variabele omhoog (oplopende lijn)
- negatieve trend: met een toename van de x-as variabele gaat de andere variabele omlaag (aflopende lijn)
- geen trend: met een toename van de ene variabele blijft de andere variabele gelijk (rechte lijn)
Als er een trend is tussen twee variabelen, hoe ziet dit verband er dan uit?
- lineair
- niet-lineair
- exponentieel
- logaritmisch
- hyperbool
Opdracht 6
- Beschrijf de onderstaande grafiek aan de hand van de 6 criteria (van les 1)
- Wat is de variatie van de meetpunten?
- Interpreteer de grafiek. Wat is je conclusie?
- Welke soort is het meest gevoelig voor caffeine?
- Op welke soort heeft het grootste effect?
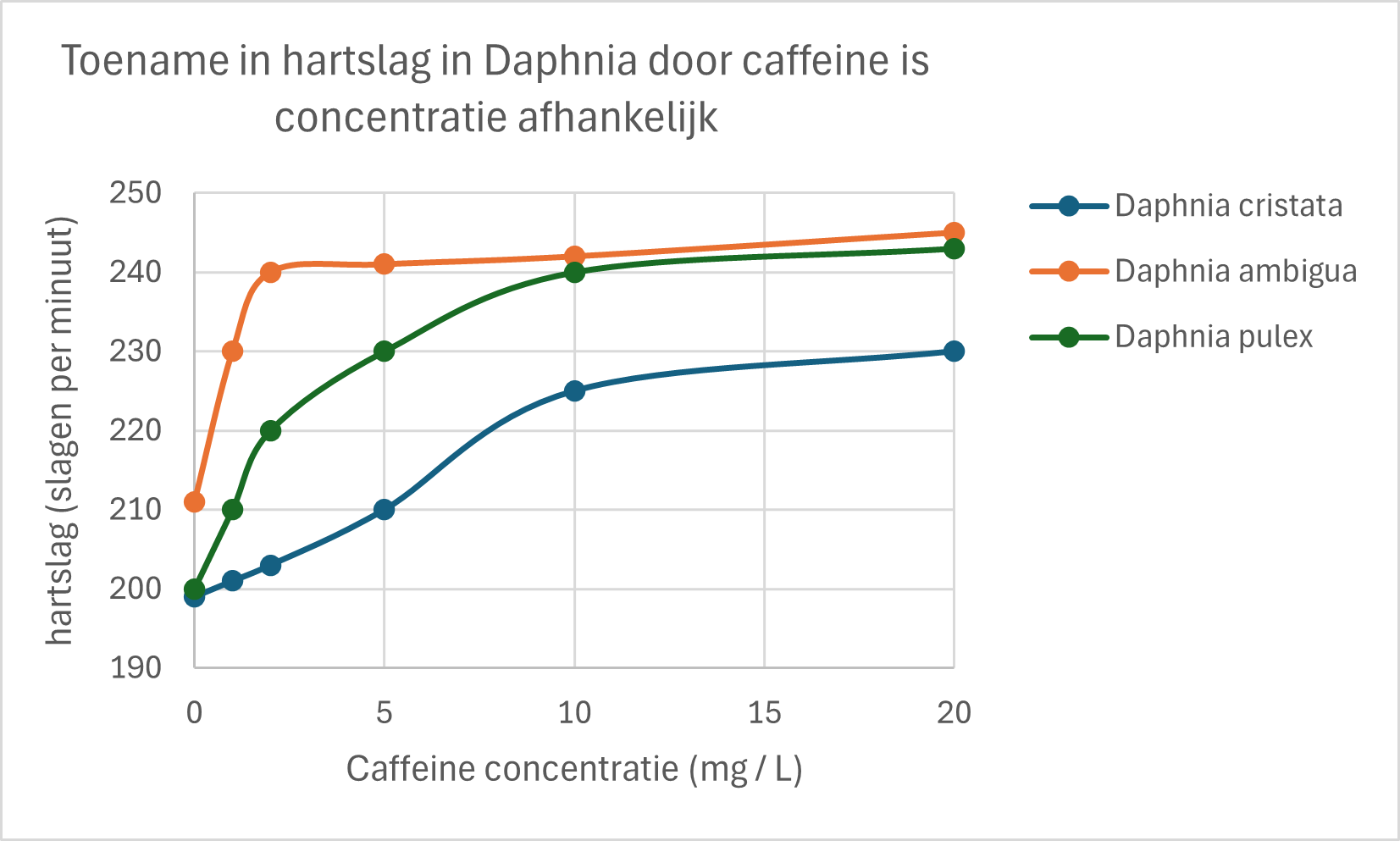
Figure 55: Watervlooien Daphnia pulex, Daphnia ambigua(n=25 voor iedere concentratie) en Daphnia cristata (n=10 voor iedere concentratie) zijn blootgesteld aan verschillende concentraties caffeine voor een tijdsduur van 30 minuten. De controle groepen zijn niet blootgesteld aan caffeine (0 mg/L). Watervlooien werden geplaatst onder een microscoop en de hartslag werd gemeten door de het aantal hartslagen te tellen voor een periode van 1 minuut.
Voor het beschrijven van de Michaelis-Menten kinetiek wordt een lijngrafiek gebruikt. De lijngrafiek laat de relatie zien tussen de concentratie van een substraat (x-as) en de reactiesnelheid (y-as) van een enzym. Deze relatie laat zien dat bij toenemende substraat concentraties de reactiesnelheid groter wordt tot het verzadigingspunt (bij toenemende substraatconcentratie is er geen toename van de reactiesnelheid). De maximale reactiesnelheid wordt de Vmax genoemd en de substraatconcentratie waarbij de helft van Vmax wordt bereikt wordt de Km genoemd.
Opdracht 6
- Beschrijf de onderstaande grafiek aan de hand van de 6 criteria (van les 1)
- Interpreteer de grafiek. Wat is je conclusie?
- Wat is de geschatte Vmax?
- Wat is de geschatte Km?
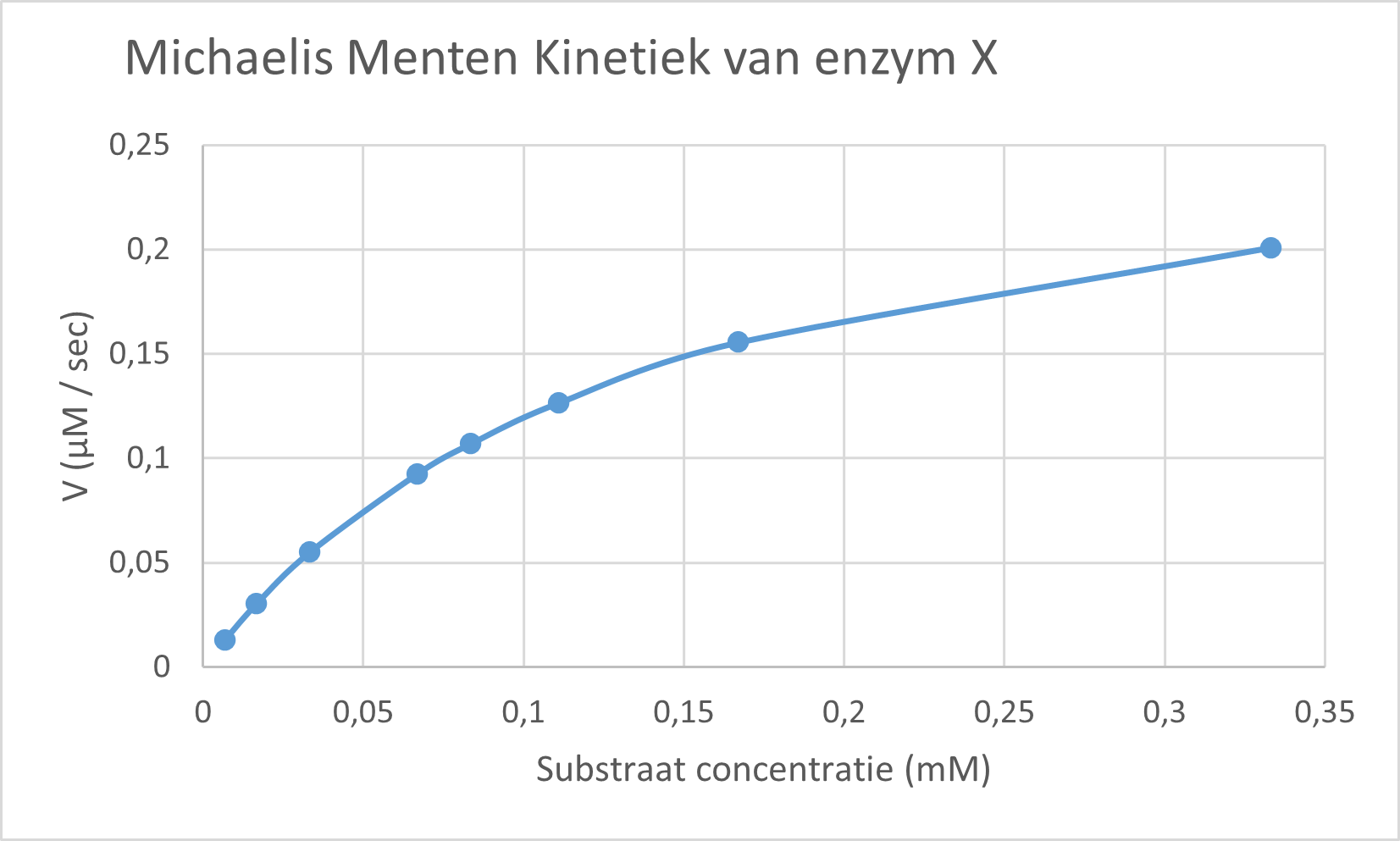
Figure 56: Michaelis-Menten kinetiek van enzym X
Deel 2: Fouten herkennen in grafieken
Meest gemaakte fouten in een grafiek
- Misleidende schalen op de assen
- ongelijke intervallen op de x-as
- gebruik van twee verschillende y-assen
- y-as begint niet vanaf 0 (resulteert in het uitvergroten van verschillen)
- Verkeerd gebruik van grafiek types
- verkeerde grafiek type
- toevoegen van 3D effecten
- Data manipulatie
- selectief laten zien van data (Cherry picking)
- weglaten van de variatie in de data
- Visuele verdichting
- teveel informatie in een grafiek
- overlappende data punten
- excessief gebruik van kleuren en patronen
Voor de onderstaande opdrachten gaan jullie in groepjes aan de slag. De opdrachten worden klassikaal nabesproken.
Opdracht 6
Open de onderstaande link
- Geef aan welke fouten er gemaakt zijn in de weergave van de grafiek zoals hierboven beschreven.
- Geef aan hoe de grafiek verbeterd kan worden.
Opdracht 6
Open de onderstaande link
- Geef aan welke fouten er gemaakt zijn in de weergave van de grafiek zoals hierboven beschreven.
- Geef aan hoe de grafiek verbeterd kan worden.
Opdracht 6
Open de onderstaande link
- Geef aan welke fouten er gemaakt zijn in de weergave van de grafiek zoals hierboven beschreven.
- Geef aan hoe de grafiek verbeterd kan worden.
Opdracht 6
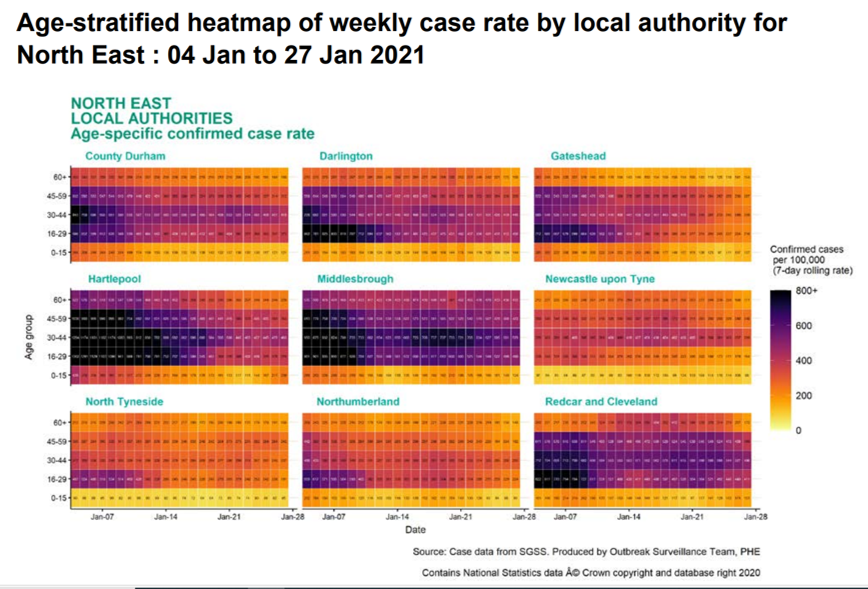
- Geef aan welke fouten er gemaakt zijn in de weergave van de grafiek zoals hierboven beschreven.
- Geef aan hoe de grafiek verbeterd kan worden.
Opdracht 6
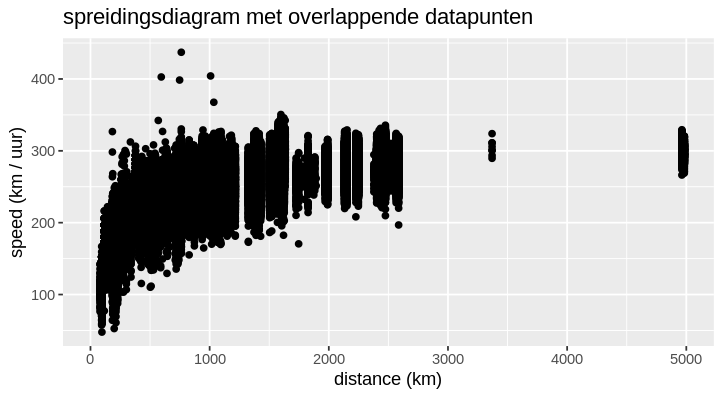
- Geef aan welke fouten er gemaakt zijn in de weergave van de grafiek zoals hierboven beschreven.
- Geef aan hoe de grafiek verbeterd kan worden.